1. Standardization (표준화)
1-1) 개요
- 다변량 분석에서는 각 컬럼의 숫자 데이터의 크기가 상대적으로 달라서 분석 결과가 왜곡되는 현상 발생
- 다변량 분석: 2개 이상의 컬럼을 같이 사용해서 수행하는 분석
- 상대적 크기 차이를 동일하게 맞추는 작업이 표준화 또는 스케일링
- 일반적으로 0 ~ 1이나 -1 ~ 1로 생성
- 방법을 달리하는 가장 큰 이유는 이상치 여부 때문
1-2) 표준값과 편차값
- 모든 값들의 표준 값 기준으로 차이를 구해서 비교
표준 값: (데이터 평균) /표준편차
- 표준 값 평균은 0, 표준 편차는 1
- 정규분포와 비교하기 쉽다.
편차 값: 표준값 * 10 + 50
- 양수로 바꿔주기. 음수는 오타나 오류를 많이 발생하고 직관적이지 않기 때문.
- 편차 값의 평균은 50, 표준 편차는 10
표준점수 해석
- 표준점수 0.0(=편차치 50) 이상은 전체의 50%
- 표준점수 1.0(=편차치 60) 이상은 전체의 15.866%
- 표준점수 2.0(=편차치 70) 이상은 전체의 2.275%
- 표준점수 3.0(=편차치 80) 이상은 전체의 0.13499%
- 표준점수 4.0(=편차치 90) 이상은 전체의 0.00315%
- 표준점수 5.0(=편차치 100) 이상은 전체의 0.00002%
students = pd.read_csv("data/student.csv", encoding='ms949', index_col ='이름') |
# 한글 폰트
import matplotlib.pyplot as plt
import platform
from matplotlib import font_manager, rc
font_name = font_manager.FontProperties(fname="c:/Windows/Fonts/malgun.ttf").get_name()
rc('font', family=font_name)
# 음수 출력 설정
plt.rcParams['axes.unicode_minus'] = False
# 표준 값 구하기
#표준값과 편차값 구하기
kormean, korstd = students['국어'].mean(), students['국어'].std()
engmean, engstd = students['영어'].mean(), students['영어'].std()
matmean, matstd = students['수학'].mean(), students['수학'].std()
students['국어표준값'] = (students['국어'] - kormean)/korstd
students['영어표준값'] = (students['영어'] - engmean)/engstd
students['수학표준값'] = (students['수학'] - matmean)/matstd
students['국어편차값'] = students['국어표준값'] * 10 + 50
students['영어편차값'] = students['영어표준값'] * 10 + 50
students['수학편차값'] = students['수학표준값'] * 10 + 50 |
students[['국어편차값','영어편차값','수학편차값']].plot(kind='bar')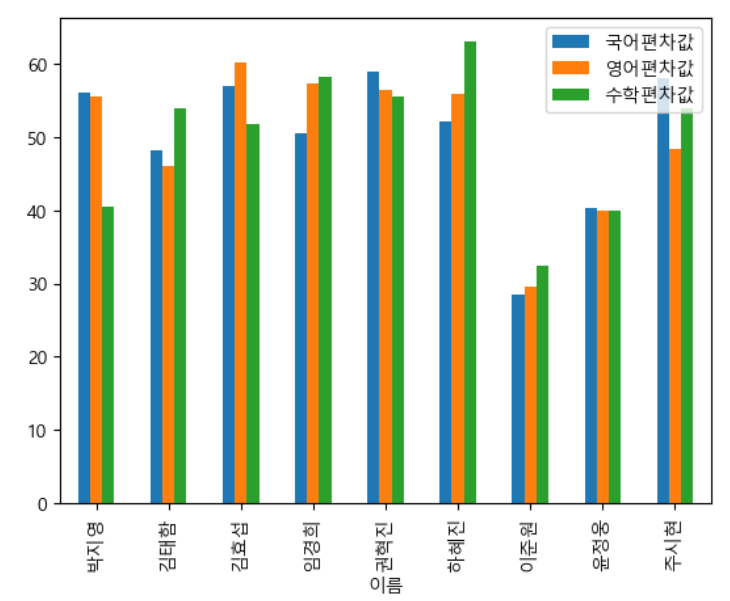 |
1-3) scikit-learn의 표준화 클래스
- StandardScaler(데이터)
- 평균이 0, 표준편차가 1이 되도록 변환
- 주성분 분석 등에서 많이 사용
- 표준화된 유사 형태의 데이터 분포로 반환
*주성분 분석: 여러 독립변수의 주된 특성만 선별하여 독립변수의 개수(=차원의 수)를 줄일 수 있다.
- MinMaxScaler(데이터)
- 특정 값에 집중되어 있는 데이터일수록 표준편차에 의한 스케일 변화 값이 커진다.
- 한쪽으로 쏠린 데이터 분포는 형태가 거의 유지된 채 범위 값이 조절된다.
- 최대값이 1, 최소값이 0이 되도록 변환
- (데이터 - 최소값) / (최대값 - 최소값)
- 신경망(딥러닝)에서 주로 사용
- RobustScaler(데이터)
- 중앙값 0, IQR이 1이 되도록 변환
- 데이터의 이상치가 많으면 평균과 표준편차에 영향을 미치기 때문에 표준화에 부정적
- 중간값과 사분위 범위를 사용하여 스케일을 조정
- (데이터 - 중간값) / (75%값 - 25%값)
- => 이상치에 덜 민감해짐
- 표준화된 유사 형태의 데이터 분포로 반환
- MaxAbsScaler(데이터)
- 0을 기준으로 절대값이 가장 큰 수가 1 또는 -1이 되도록 변환
- 절대값이 0 ~ 1 사이가 되도록 매핑
- 각 열 별로 절대값이 가장 큰 값으로 나누는 것
- 양수 데이터로만 구성된 경우에는 MinMax와 유사하면 이상치에 민감
- 음수 자체가 어떤 의미를 지닌 경우 사용
- QuantileTransformer
- 데이터를 1000개의 분위로 나눠 0 ~ 1 사이에 고르게 분포시키는 방식
- 이상치의 영향을 제거하기 어려운 경우 사용. 이상치의 영향을 덜 받게 해줌
이상치를 제거하는게 맞을까, 영향을 줄이는 게 맞을까, 이상치끼리 분석해주는게 맞을까?
어쩔 수 없이 이상치를 가지고 분석해야 하는 경우 이렇게 스케일링을 해줘야 한다.
그래서 먼저 데이터를 그래프로 그려보고 박스플롯이나 분산차트 같은 걸로 이상치를 확인한다.
전처리는 scikit-learn으로 거의 다 됨
스케일링 시 Feature 별로 크기를 유사하게 만드는 것은 중요하지만, 특성에 따라 어떤 항목은 데이터의 분포를 유지해야 한다. 데이터가 한 곳에 집중된 Feature를 표준화시키면 작은 단위 변화가 큰 차이를 나타내는 것처럼 반영되기 때문이다.
- 표준화 과정
- 데이터를 입력해서 fit 메소드 호출 - 분포 모수를 객체 내에 저장
- 데이터를 입력해서 transform 메소드 호출 - 표준화된 결과 리턴
- 2개의 과정을 합친 fit_transform 메소드도 있다.
- 훈련 세트와 테스트 세트로 나눈 경우 동일한 방식으로 표준화 작업
from sklearn import preprocessingx = mpg[['horsepower']].values
#표준화 전의 기술통계 값
print('평균:', np.mean(x))
print('표준 편차:', np.std(x))
print('최대값:', np.max(x))
print('최소값:', np.min(x))| 평균: 104.46938775510205 표준 편차: 38.44203271442593 최대값: 230.0 최소값: 46.0 |
#평균 0, 표준편차 1로 만드는 스케일링 - StandardScaler
scaler = preprocessing.StandardScaler()
scaler.fit(x)
x_scaled = scaler.transform(x)
print('평균:', np.mean(x_scaled))
print('표준 편차:', np.std(x_scaled))
print('최대값:', np.max(x_scaled))
print('최소값:', np.min(x_scaled))| 평균: -1.812609019796174e-16 표준 편차: 0.9999999999999998 최대값: 3.2654519904664348 최소값: -1.5209754434541274 |
# 이상치가 많은 경우 - RobustScaler
scaler = preprocessing.RobustScaler()
scaler.fit(x)
x_scaled = scaler.transform(x)| 평균: 0.2150860344137655 표준 편차: 0.7537653473416848 최대값: 2.676470588235294 최소값: -0.9313725490196079 |
| 표준화 전 | 표준화 후 |
 |
 |
2. Normalization (정규화)
- 데이터 범위를 0과 1로 변환해서 데이터 분포 조정
- scikit-learn의 Normalizer 클래스의 객체를 만든 후 transform 함수 사용
- norm 옵션: L1, L2를 설정
- L1: 맨해튼 거리
- 각 좌표 거리의 합. 지도상에 보이는 경로 같은 거.
- L2: 유클리드 거리
- 각 좌표를 빼서 제곱하고 더한 다음에 루트 .. 그냥 대각선으로 가는 것
- 여러 개의 속성을 한꺼번에 스케일링
- 행 단위로 스케일링
- 여러 개의 컬럼을 가진 데이터(텍스트)에서 컬럼들이 독립적이지 않은 경우 이용
from sklearn.preprocessing import Normalizer# 특성 행렬을 만듭니다.
features = np.array([[1, 2],
[2, 3],
[3, 8],
[4, 2],
[7, 2]])
# 정규화 객체 생성
normalizer = Normalizer(norm="l1")
# 특성 행렬을 변환
features_l1_norm = normalizer.transform(features)
print(features_l1_norm)| [[0.33333333 0.66666667] [0.4 0.6 ] [0.27272727 0.72727273] [0.66666667 0.33333333] [0.77777778 0.22222222]] |
- l1은 행 데이터의 합을 가지고 각 데이터를 나눈 값: 총계 1
normalizer = Normalizer(norm="l2")
features_l2_norm = normalizer.transform(features)
print(features_l2_norm)| [[0.4472136 0.89442719] [0.5547002 0.83205029] [0.35112344 0.93632918] [0.89442719 0.4472136 ] [0.96152395 0.27472113]] |
- l2를 설정하면 각 데이터를 제곱해서 더한 값의 제곱근
# max
normalizer = Normalizer(norm = "max")
features_l1_norm = normalizer.transform(features)
print(features_l1_norm)| [[0.5 1. ] [0.66666667 1. ] [0.375 1. ] [1. 0.5 ] [1. 0.28571429]] |
3. 다항 특성과 교차항 특성
- 다항: 제곱해나가는 것
- 교차항: 곱하는 것
- 컬럼들을 제곱하고 곱해서 데이터 추가
- 특성과 타겟 사이에 비선형 관계가 존재하는 경우 다항 특성 생성
- scikit-learn의 PolynomialFeatures 클래스 이용
- degree 옵션: 몇차 항까지 생성할 것인지 설정
- include_bias 옵션: 첫번째 항으로 상수 1을 추가할지 여부 설정
- interation_only 옵션: True를 설정하면 교차항 특성만 생성
- 생성된 객체의 get_feature_names_out 함수를 이용하면 변환식 이름으로 반환
from sklearn.preprocessing import PolynomialFeatures# 특성 행렬을 만든다.
features = np.array([[2, 3],
[1, 2],
[22, 6]])
# PolynomialFeatures 객체를 만든다.
polynomial_interaction = PolynomialFeatures(degree=2, include_bias=False)
# 다항 특성을 만든다.
result = polynomial_interaction.fit_transform(features)
print(result)| [[ 2. 3. 4. 6. 9.] [ 1. 2. 1. 2. 4.] [ 22. 6. 484. 132. 36.]] |
polynomial_interaction = PolynomialFeatures(degree=2, include_bias=True, interaction_only=True)
result = polynomial_interaction.fit_transform(features)
print(result)| [[ 1. 2. 3. 6.] [ 1. 1. 2. 2.] [ 1. 22. 6. 132.]] |
4. 특성 변환
- 컬럼에 함수를 적용해서 데이터를 변경
- pandas의 apply 함수 이용
- API: sklean.FunctionTransformer, sklean.ColumnTransformer
- FunctionTransformer: 모든 열에 동일한 함수 적용하고자 할 때 사용
- = pandas.apply
- ColumnTransformer: 각 열에 다른 함수 적용하고자 할 때 사용
- 함수, 변환기, 컬럼 이름의 리스트로 이루어진 튜플의 list를 매개변수로 받음
- pandas는 데이터가 Series나 DataFrame
- scikit-learn은 데이터가 numpy의 ndarray, 특별한 경우가 아니면 2차원 배열
#함수를 적용해서 데이터 변경
from sklearn.preprocessing import FunctionTransformer
features = np.array([[1, 3],
[3, 6]])
def add_one(x:int) -> int:
return x + 1
one_transformer = FunctionTransformer(add_one)
result = one_transformer.transform(features)
print(result)| [[2 4] [4 7]] |
df = pd.DataFrame(features, columns = ['f1', 'f2'])
print(df.apply(add_one))| f1 f2 0 2 4 1 4 7 |
5. 숫자 데이터의 이산화
- 데이터를 분석할 때 연속된 데이터는 일정한 구간으로 나눠서 분석하는 것이 효율적
- ex. 가격, 비용, 효율, 나이 등
- 연속적인 값을 일정한 수준이나 정도를 나타내는 이산적인 값으로 나타내어 구간별 차이를 드러나게 함
5-1) 구간 분할
- 연속형 데이터를 일정한 구간으로 나누고 각 구간을 범주형 이산 변수로 치환하는 과정 : binning (구간 분할)
- pandas의 cut 함수: 연속형 데이터를 여러 구간으로 분할해서 범주형 데이터로 변환가능
- 구간을 분할할 때 반드시 일정한 간격을 만들 필요는 없음
10대는 쪼개서 분류하는게 좋다.
df = pd.read_csv('./data/auto-mpg.csv', header=None)
# 열 이름을 설정
df.columns = ['mpg','cylinders','displacement','horsepower','weight',
'acceleration','model year','origin','name']
df['horsepower'].replace('?', np.nan, inplace=True) # '?'을 np.nan으로 변경
df.dropna(subset=['horsepower'], axis=0, inplace=True) # 누락데이터 행을 삭제
df['horsepower'] = df['horsepower'].astype('float') # 문자열을 실수형으로 변환
# 구간 분할
count, bin_dividers = np.histogram(df['horsepower'], bins=3)
print(count)
print(bin_dividers)| [257 103 32] [ 46. 107.33333333 168.66666667 230. ] |
- 모든 함수는 데이터를 하나만 리턴할 수 있다.
- 튜플은 튜플을 리턴할 때 나누어서 할당이 가능
# 3개의 bin에 이름 지정
bin_names = ['저출력', '보통출력', '고출력']
# pd.cut 함수로 각 데이터를 3개의 bin에 할당
df['hp_bin'] = pd.cut(x=df['horsepower'], # 데이터 배열
bins=bin_dividers, # 경계 값 리스트
labels=bin_names, # bin 이름
include_lowest=True) # 첫 경계값 포함 여부
df[['horsepower', 'hp_bin']].head(20) |
- numpy. digitize
- 첫번째 데이터는 이산화할 데이터
- bins = 이산화할 경계값 리스트
- right = 경계값 포함 여부 설정
- sklearn. Binarizer
- 생성할 때 하나의 경계값을 대입해서 생성하고 fit_transform을 호출하면
경계값보다 작은 경우는 0, 그렇지 않은 경우는 1을 할당해서 리턴
- sklearn. KBinsDiscretizer
- 첫번째 매개변수: 구간 개수
- encode: ordinal(각 구간을 하나의 컬럼에 일련번호 형태 리턴), onehot(희소 행렬 리턴), onehot-dense(밀집 행렬 형태 리턴)
- strategy: quantile(일정한 비율), uniform(구간 폭 일정)
- bin_edges_: 각 구간의 값을 알고자 할 때 속성 확인
Label Encoding: 순서가 의미 있을 때 (0, 1, 2)
OneHot Encoding: 순서가 의미 없을 때
- Sparse Matrix (희소 행렬): 행렬 전체 반환
- Dense Matrix (밀집 행렬): 값의 위치만 반환
a = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]]
pandas의 메소드들은 DataFrame이나 Series를 이용해서 작업하지만
Machine Learning 관련된 메소드들은 2차원 이상의 ndarray로 작업
# pandas.cut()
age = np.array([[13],
[30],
[67],
[36],
[64],
[24]])
# 30을 기준으로 분할
result = np.digitize(age, bins=[30])
print(result)| [[0] [1] [1] [1] [1] [0]] |
- 30이 안되면 0 / 30 이상이면 1로 변환
- bins에는 여러개의 데이터 설정이 가능
#0-19, 20-29, 30-63, 64이상의 구간으로 분할
result = np.digitize(age, bins=[20,30,64])
print(result)| [[0] [2] [3] [2] [3] [1]] |
#0-20, 21-30, 31-64, 64초과 구간으로 분할
result = np.digitize(age, bins=[20,30,64], right=True)
print(result)
print()| [[0] [1] [3] [2] [2] [1]] |
# Binarizer를 이용한 구간 분할
from sklearn.preprocessing import Binarizer
#threshold(임계값)
binarizer = Binarizer(threshold=30.0)
print(binarizer.transform(age))- 흑백 이미지 데이터에서 뚜렷한 구분을 위해 임계값 아래와 위를 구분
| [[0] [0] [1] [1] [1] [0]] |
# KBinsDiscretizer를 이용한 구간 분할
from sklearn.preprocessing import KBinsDiscretizer
#균등한 분포로 4분할
#ordinal: 라벨 인코딩 - 일련번호
kb = KBinsDiscretizer(4, encode='ordinal', strategy='quantile')
print(kb.fit_transform(age))
print()
#원핫인코딩을 해서 희소 행렬로 표현
kb = KBinsDiscretizer(4, encode='onehot', strategy='quantile')
print(kb.fit_transform(age))
print()
#원핫인코딩을 해서 밀집 행렬로 표현
kb = KBinsDiscretizer(4, encode='onehot-dense', strategy='quantile')
print(kb.fit_transform(age))| [[0.] [1.] [3.] [2.] [3.] [0.]] (0, 0) 1.0 (1, 1) 1.0 (2, 3) 1.0 (3, 2) 1.0 (4, 3) 1.0 (5, 0) 1.0 [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 0. 1.] [0. 0. 1. 0.] [0. 0. 0. 1.] [1. 0. 0. 0.]] |
5-2) 군집 분석
- 2개 이상의 컬럼의 값으로 이산화
- 데이터 전처리 단계에서 군집 분석한 결과를 기존 데이터의 컬럼으로 추가해서 이산화 수행 가능
- 수집 -> 전처리 -> 분석 *순서는 언제든지 변경되고 나선형으로 수행될 수 있음
- k 개의 그룹이 있다는 것을 아는 경우에는 k-means clustering을 사용하여 비슷한 샘플을 그룹화 할 수 있음
from sklearn.cluster import KMeans# 모의 특성 행렬을 생성
sample = np.array([[13, 30],
[30, 40],
[67, 44],
[36, 24],
[64, 37],
[24, 46]])
# 데이터프레임을 생성
dataframe = pd.DataFrame(sample, columns=["feature_1", "feature_2"]) |
# k-평균 군집 모델을 생성
clusterer = KMeans(3, random_state=42)
# 모델을 훈련
clusterer.fit(sample)
# 그룹 소속을 예측
dataframe["group"] = clusterer.predict(sample)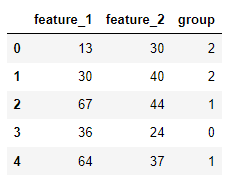 |
6. 이상치 탐지
- Z-score 이용
- 중앙값을 기준으로 표준 편차가 절대값 3 범위의 바깥 쪽에 위치하는 데이터를 이상치로 간주
- 데이터가 12개 이하이면 이상치 감지 불가

- Z-score 보정
- 편차의 절대값 범위를 3.5로 설정한 후 0.6745를 곱해서 사용
- IQR(3사분위수 - 1사분위수)
- 1사분위수보다 1.5(IQR) 이상 작은 값이나 3사분위수보다 1.5(IQR) 이상 큰 값을 이상치로 간주
- boxplot에서 수염 바깥쪽 데이터를 이상치로 간주

- 투표: 3개 모두 사용해보고 2개 이상에서 이상치로 간주되는 데이터를 이상치 판정
- 데이터의 특정 비율을 이상치로 간주
- scikit-learn의 covariance.EllipticEnvelope 클래스 이용
- 잘 제시되지는 않는 방법
- 수식을 이용한 이상치 탐지
#이상치 탐지를 위한 데이터 생성
features = np.array([[10, 10, 7, 6, 4, 4, 3,3],
[20000, 3, 5, 9, 2, 2, 2, 2]])
# Z-score 이용
def outliers_z_score(ys):
threshold = 3
mean_y = np.mean(ys)
print("평균:", mean_y)
stdev_y = np.std(ys)
print("표준 편차:", stdev_y)
z_scores = [(y - mean_y) / stdev_y for y in ys]
print("z_score:", z_scores)
return np.where(np.abs(z_scores) > threshold)| 평균: 1254.5 표준 편차: 4840.068065120572 z_score: [array([-0.25712448, -0.25712448, -0.25774431, -0.25795092, -0.25836414, -0.25836414, -0.25857074, -0.25857074]), array([ 3.87298272, -0.25857074, -0.25815753, -0.25733109, -0.25877735, -0.25877735, -0.25877735, -0.25877735])] (array([1], dtype=int64), array([0], dtype=int64)) |
- 하지만 데이터가 12개 이하면 null 값이 뜬다.
# Z-score 보정 - 데이터 개수에 상관없이 이상치 감지
def outliers_modified_z_score(ys):
threshold = 3.5
#중앙값 구하기
median_y = np.median(ys)
#중위 절대편차 구함
median_absolute_deviation_y = np.median([np.abs(y - median_y) for y in ys])
#중위 절대 편차를 가지고 계산한 후 0.6745 곱하기
#결과가 3.5보다 크면 이상치로 감지
modified_z_scores = [0.6745 * (y - median_y) / median_absolute_deviation_y
for y in ys]
return np.where(np.abs(modified_z_scores) > threshold)| (array([1], dtype=int64), array([0], dtype=int64)) |
- 데이터가 12개 이하여도 상관없음
# IQR
def outliers_iqr(ys):
#1사분위, 3사분위
quartile_1, quartile_3 = np.percentile(ys, [25, 75])
#IQR
iqr = quartile_3 - quartile_1
#하한과 상한 구하기
lower_bound = quartile_1 - (iqr * 1.5)
upper_bound = quartile_3 + (iqr * 1.5)
print("하한값:", lower_bound)
print("상한값:", upper_bound)
return np.where((ys > upper_bound) | (ys < lower_bound))
features = np.array([[10, 10, 7, 6, -4900],
[20000, 3, 5, 9, 10]])
print(outliers_iqr(features))| 하한값: -1.875 상한값: 17.125 (array([0, 1], dtype=int64), array([4, 0], dtype=int64)) |
print(outliers_iqr(df['horsepower'].values))| 하한값: -1.5 상한값: 202.5 (array([ 6, 7, 8, 13, 25, 27, 66, 93, 94, 115], dtype=int64),) |
# 일정한 비율의 데이터를 이상치로 간주
- 값보다는 비율을 이용해서 이상치 판정
- ex. 국가장학금 지급할 때 특정한 소득 기준은 없고 상위 10%를 제외한 학생에게 장학금을 지급하는 경우
#일정한 비율을 이상치로 간주하는 API
from sklearn.covariance import EllipticEnvelope
#데이터를 생성해주는 API
from sklearn.datasets import make_blobs# 모의 데이터를 만듭니다.
features, _ = make_blobs(n_samples = 10,
n_features = 2,
centers = 1,
random_state = 1)| [[-1.83198811 3.52863145] [-2.76017908 5.55121358] [-1.61734616 4.98930508] [-0.52579046 3.3065986 ] [ 0.08525186 3.64528297] [-0.79415228 2.10495117] [-1.34052081 4.15711949] [-1.98197711 4.02243551] [-2.18773166 3.33352125] [-0.19745197 2.34634916]] |
# 첫 번째 샘플을 극단적인 값으로 바꾼다.
features[0,0] = 10000
features[0,1] = 10000
print(features)
# 이상치 감지 객체 - 10%는 이상치로 간주
outlier_detector = EllipticEnvelope(contamination=0.1)
# 감지 객체를 훈련
outlier_detector.fit(features)
# 이상치를 예측 - (-1)이면 이상치, (1)이면 정상
outlier_detector.predict(features)| [[ 1.00000000e+04 1.00000000e+04] [-2.76017908e+00 5.55121358e+00] [-1.61734616e+00 4.98930508e+00] [-5.25790464e-01 3.30659860e+00] [ 8.52518583e-02 3.64528297e+00] [-7.94152277e-01 2.10495117e+00] [-1.34052081e+00 4.15711949e+00] [-1.98197711e+00 4.02243551e+00] [-2.18773166e+00 3.33352125e+00] [-1.97451969e-01 2.34634916e+00]] array([-1, 1, 1, 1, 1, 1, 1, 1, 1, 1]) |
# 연습문제
- 파일은 공백으로 구분
- 첫번째 데이터는 접속한 컴퓨터의 IP, 마지막 데이터는 트래픽
전체 트래픽의 합계 구하기
IP별 트래픽의 합계 구하기
#전체 트래픽의 합계 구하기
# 파일 불러오기
with open('./data/log.txt', 'r') as f:
data = f.readlines()
# 공백 기준으로 데이터 분리하기
data_split = [x.strip().split() for x in data[1:]]
# 데이터프레임 생성, 열 이름 지정
df = pd.DataFrame(data_split, columns=['IP', 'x', 'x', 'datetime', 'um', 'GET/POST', 'path', 'port', 'server', 'traffic'])
# 필요없는 컬럼 제거
df = df.drop('x', axis=1)
# 트래픽 계산에 방해되는 놈들 제거
df['traffic'].replace('-', np.nan, inplace=True)
df['traffic'].replace('"-"', np.nan, inplace=True)
df = df.dropna()
# 트래픽 정수형 형변환
df.traffic = df.traffic.astype('int')
# 전체 트래픽 합계
nan.traffic.sum()
# IP별 트래픽의 합계 구하기
#IP별로 그룹화
grouped = df.groupby(['IP'])
ip_sum = grouped.sum()
=> Comprehension
Comprehension
r = []
for i in L:
r.append(i**2)
print(r)
#map
r = list(map(lambda x:x**2, L))
print(r)
#list comprehension
r = [i**2 for i in L]
print(r)
#필터링 : L의 모든 데이터를 i에 순차적으로 대입하고 조건문이 참인 경우만 list 생성
r = [i for i in L if i % 2 == 0]
print(r)| [0, 1, 4, 9, 16, 25, 36, 49, 64, 81] [0, 1, 4, 9, 16, 25, 36, 49, 64, 81] [0, 1, 4, 9, 16, 25, 36, 49, 64, 81] [0, 2, 4, 6, 8] |
li1 = [1, 2, 3]
li2 = [1, 2, 3]
#for 안에 for 사용
#먼저 나온 for가 바깥쪽, 뒤에 나온 for가 안쪽
r = [x * y for x in li1 for y in li2]
print(r)| [1, 2, 3, 2, 4, 6, 3, 6, 9] |
7. 텍스트 데이터
7-1) 한글 형태소 분석
형태소 분석기 설치 - konlpy
- JDK(자바 개발 도구)를 설치
JAVA_HOME 환경 변수에 JDK 경로를 설정
PATH에 JDK의 bin 디렉토리 경로를 설정: Java 명령어를 콘솔에서 편리하게 사용하기 위해서
- Windows 의 경우에는 Visual C++ 재배포 패키지 설치
Visual Studio 의 데스크톱 애플리케이션 개발 을 설치해도 됨
- Jpype-1 패키지 설치
Python 3.11: pip install Jpype1-py3
Python 3.12: pip install Jpype1
- 형태소 분석을 하는 이유
- 우리나라는 공백 단위로 분할을 해서는 단어를 만들 수 없기 때문에 공백 단위로 쪼개고 어간 추출 필요
- 데이터 분석을 하다보면 특정 품사의 데이터만 필요한 경우가 발생
- 한글 형태소 분석기 모듈
- Hannanum
- Kkma
- Komoran
- Mecab
- Okt
- Twitter (최근에는 사용을 권장하지 않음)
#형태소 분석할 문장
text = "태양계는 지금으로부터 약 46억년 전 거대한 분자구름의 일부분이 중력붕괴를 일으키면서 형성되었다."
#자연어 처리를 할 때 공백 단위로 토큰화 하는 것은 큰 의미가 없음
#공백 단위로 토큰화하는 것은 로그 분석을 할 때 입니다.
data = text.split(' ')
print(data)| ['태양계는', '지금으로부터', '약', '46억년', '전', '거대한', '분자구름의', '일부분이', '중력붕괴를', '일으키면서', '형성되었다.'] |
from konlpy.tag import Kkma
kkma = Kkma()
#문장 분석 - 하나의 텍스트에 마침표가 있는 경우 분할
print(kkma.sentences(text))
#단어별 분석 - 명사만 추출
print(kkma.nouns(text))
#형태소 분석 - 품사를 같이 제공: 이 작업을 수행하는 것을 품사 태깅 - 자연어 처리의 한 분야
print(kkma.pos(text))| ['태양계는 지금으로부터 약 46억 년 전 거대한 분자 구름의 일부분이 중력 붕괴를 일으키면서 형성되었다.'] ['태양계', '지금', '46', '46억년', '억', '년', '전', '거대', '분자', '분자구름', '구름', '일부분', '중력', '중력붕괴', '붕괴', '형성'] [('태양계', 'NNG'), ('는', 'JX'), ('지금', 'NNG'), ('으로', 'JKM'), ('부터', 'JX'), ('약', 'MDN'), ('46', 'NR'), ('억', 'NR'), ('년', 'NNB'), ('전', 'NNG'), ('거대', 'NNG'), ('하', 'XSV'), ('ㄴ', 'ETD'), ('분자', 'NNG'), ('구름', 'NNG'), ('의', 'JKG'), ('일부분', 'NNG'), ('이', 'JKS'), ('중력', 'NNG'), ('붕괴', 'NNG'), ('를', 'JKO'), ('일으키', 'VV'), ('면서', 'ECE'), ('형성', 'NNG'), ('되', 'XSV'), ('었', 'EPT'), ('다', 'EFN'), ('.', 'SF')] |
from konlpy.tag import Hannanum
hannanum = Hannanum()
print(hannanum.nouns(text))
#사용하는 단어 사전이 다르므로 앞의 결과와 다른 결과가 나올 수 있습니다.
print(hannanum.pos(text))
from konlpy.tag import Okt| ['태양계', '지금', '약', '46억년', '전', '거대', '분자구름', '일부분', '중력붕괴', '형성'] [('태양계', 'N'), ('는', 'J'), ('지금', 'N'), ('으로부터', 'J'), ('약', 'N'), ('46억년', 'N'), ('전', 'N'), ('거대', 'N'), ('하', 'X'), ('ㄴ', 'E'), ('분자구름', 'N'), ('의', 'J'), ('일부분', 'N'), ('이', 'J'), ('중력붕괴', 'N'), ('를', 'J'), ('일으키', 'P'), ('면서', 'E'), ('형성', 'N'), ('되', 'X'), ('었다', 'E'), ('.', 'S')] |
7-2) BoW (Bag of Word)
- 텍스트 데이터에서 특정 단어의 등장 횟수를 나타내는 특성을 만드는 작업
- 워드클라우드처럼 등장 횟수를 이용해서 시각화를 위해서 수행하고너 단어별 가중치를 적용하기 위해서 작업을 수행
- scikit-learn 의 CountVectorizer 클래스를 이용해서 인스턴스를 생성하고 fit_transform 함수에 문자열을 대입하면 BoW 특성 행렬을 만들어주고 to_array 함수를 호출하면 밀집 행렬로 결과를 리턴합니다.
- 인스턴스를 생성할 때 사용할 수 있는 옵션
- ngram_range: 정수 형태의 튜플을 대입하면 ngram(단어가 연속으로 등장하는 경우 하나의 단어로 취급) 옵션 설정 가능
- stop_words: 불용어 설정
- vocabulary: 횟수를 계산할 단어의 list
- max_df: 최대 개수
- min_df: 최소 개수
- max_feature: 상위 몇 개의 단어만 추출
- 인스턴스의 속성: get_feature_names()를 호출하면 각 특성에 연결된 단어를 확인
- 단어 별 빈도수 확인
#샘플 데이터 생성
import numpy as np
import pandas as pd
text_data = np.array(['I love Newziland newziland',
'Sweden is best',
'Korea is not bad',
'Python Python Java Python R Java C'])
from sklearn.feature_extraction.text import CountVectorizer
#BoW 객체를 생성
#모든 문자열을 소문자로 변경해서 수행
#알파벳 한글자는 모두 제거
countVectorizer = CountVectorizer()
bag_of_words = countVectorizer.fit_transform(text_data)
#희소 행렬
print(bag_of_words)
#밀집 행렬
print(bag_of_words.toarray())
#각 열의 의미
print(countVectorizer.get_feature_names_out())| [[0] [0] [0] [0]] ['newziland, korea'] |
7-3) 단어 별 가중치 적용
tf-idf(term frequency - inverse document frequency)를 이용한 가중치 계산
가중치를 계산할 때는 tf * idf
- idf = log((1 + 문서의개수)/1+등장한문서빈도) + 1
- 여러 문서에서 등장하는 단어가 있다면 이 단어는 중요하지 않을 가능성이 높음
- tf = 하나의 문서에서 등장한 빈도 수
- 하나의 문서에 어떤 단어가 많이 등장할수록 중요한 단어
text_data = np.array(['I love Newziland newziland',
'Sweden is best',
'Korea is not bad',
'Python Python Java Python R Java C'])
#단어별 가중치 확인
from sklearn.feature_extraction.text import TfidfVectorizer
tfidfVectorizer = TfidfVectorizer()
feature_matrix = tfidfVectorizer.fit_transform(text_data)
print(tfidfVectorizer.vocabulary_)
print(feature_matrix.toarray())
| {'love': 5, 'newziland': 6, 'sweden': 9, 'is': 2, 'best': 1, 'korea': 4, 'not': 7, 'bad': 0, 'python': 8, 'java': 3} [[0. 0. 0. 0. 0. 0.4472136 0.89442719 0. 0. 0. ] [0. 0.61761437 0.48693426 0. 0. 0. 0. 0. 0. 0.61761437] [0.52547275 0. 0.41428875 0. 0.52547275 0. 0. 0.52547275 0. 0. ] [0. 0. 0. 0.5547002 0. 0. 0. 0. 0.83205029 0. ]] |
8. 시계열 데이터
- 날짜와 시간을 이용해서 정렬된 데이터
- 일정한 패턴을 가진 데이터도 시계열 데이터로 간주
- 물리적 흔적: 의학, 청각학 또는 기상학 등에서 측정한 물리적 흔적
8-1) pandas의 시계열 자료형
- datetime64(TimeStamp)
- 시계열 데이터를 저장하기 위한 자료형
- tz 옵션: 시간대 설정 가능
- 부등호 이용해서 크기 비교 가능
- 뺄셈 수행해서 간격 확인 가능
- Period
- 두 시점 사이의 일정한 기간을 나타내는 자료형
- 데이터를 생성할 때 많이 이용
8-2) 자료형 변환
- 문자열 데이터를 datetime64로 변환
- pandas.to_datetime 함수 이용
- 날짜 형식의 문자열과 format 매개변수에 날짜 형식을 지정해서 생성하는데 format을 생략하면 유추
- errors 매개변수에 ignore를 설정하면 에러가 발생했을 때 문자열을 그대로 리턴, coerce를 설정하면 문제가 발생할 때 NaT를 설정하며 raise를 설정하면 예외를 발생시켜서 중단

df = pd.read_csv("./data/stock-data.csv")
df.info()| <class 'pandas.core.frame.DataFrame'> RangeIndex: 20 entries, 0 to 19 Data columns (total 6 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Date 20 non-null object 1 Close 20 non-null int64 2 Start 20 non-null int64 3 High 20 non-null int64 4 Low 20 non-null int64 5 Volume 20 non-null int64 dtypes: int64(5), object(1) memory usage: 1.1+ KB |
- 현재는 Date 컬럼이 object - 문자열
df['NewDate'] = pd.to_datetime(df['Date'])
df.info()| ... 0 Date 20 non-null object ... |
- 데이터를 출력해보면 Date 와 NewDate는 구분이 안되지만 자료형을 확인하면 다름
#데이터를 출력해보면 Date 와 NewDate는 구분이 안되지만 자료형을 확인하면 다름
print(df.head())
#연속된 날짜는 인덱스로 많이 사용
df.set_index('NewDate', inplace=True)
print(df.head())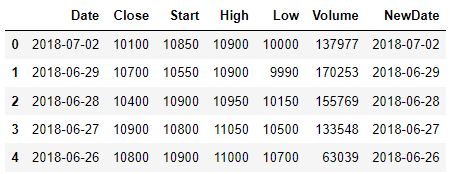 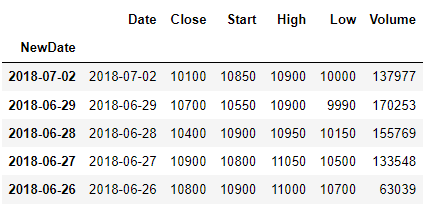 |
8-3) Period
- to_period 함수를 이용해서 Timestamp 객체를 일정한 기간을 나타내는 Period 객체로 변환 가능
- freq 옵션: 기준이 되는 기간 설정

dates = ['2017-01-01', '2018-06-03', '2019-11-02']
#문자열을 Timestamp로 변경
pddates = pd.to_datetime(dates)
print(pddates)| DatetimeIndex(['2017-01-01', '2018-06-03', '2019-11-02'], dtype='datetime64[ns]', freq=None) |
#월로 변경 - 모든 날짜가 월 초 나 월 말로 변경
pr_months = pddates.to_period(freq='M')
print(pr_months)| PeriodIndex(['2017-01', '2018-06', '2019-11'], dtype='period[M]', freq='M') |
#분기로 변경
pr_months = pddates.to_period(freq='Q')
print(pr_months)| PeriodIndex(['2017Q1', '2018Q2', '2019Q4'], dtype='period[Q-DEC]', freq='Q-DEC') |
8-4) date_range
- 일정한 간격을 맞는 시계열 데이터 생성 함수
- 매개변수
- start: 시작 날짜
- end: 종료 날짜
- periods: 생성할 데이터 개수
- freq: 간격
- tz: 시간대 설정('Asia/Seoul')
# 2024년 1월 1일 부터 일 단위로 30개의 데이터를 생성
ts_ms = pd.date_range(start='2024-01-01', end=None, periods=30, freq='D')
print(ts_ms)| DatetimeIndex(['2024-01-01', '2024-01-02', '2024-01-03', '2024-01-04', '2024-01-05', '2024-01-06', '2024-01-07', '2024-01-08', '2024-01-09', '2024-01-10', '2024-01-11', '2024-01-12', '2024-01-13', '2024-01-14', '2024-01-15', '2024-01-16', '2024-01-17', '2024-01-18', '2024-01-19', '2024-01-20', '2024-01-21', '2024-01-22', '2024-01-23', '2024-01-24', '2024-01-25', '2024-01-26', '2024-01-27', '2024-01-28', '2024-01-29', '2024-01-30'], dtype='datetime64[ns]', freq='D') |
8-5) 날짜 데이터의 분리
- pandas 의 Series 의 dt.단위를 이용
- year, month, day, hour, minute, weekday(월요일이 0) 를 이용
8-6) 시차 특성을 갖는 데이터 생성
- shift(간격, freq)를 이용하는데 이 함수는 pandas의 Series의 함수
df = pd.read_csv("./data/stock-data.csv")
df['NewDate'] = pd.to_datetime(df['Date'])- 년도만 추출해보면
print(df['NewDate'].dt.year)| 0 2018 1 2018 2 2018 3 2018 ... Name: NewDate, dtype: int64 |
- 이 경우는 간격이 하루 단위가 아니라서 앞의 데이터가 밀려들어오는 것처럼 보이지 않는데 전부 하루 간격이라면 밀려들어온다.
print(ts.shift(-1))| NewDate 2018-07-02 0.579450 2018-06-29 -0.774314 2018-06-28 0.650039 ... |
8-7) 결측치 처리
- 누락된 데이터의 기간을 삭제하거나
- 대체(Imputation)법: 관측에 기반에서 누락된 데이터를 채워넣는 방법
- 누락된 데이터의 이전이나 이후값으로 채워넣는 방식
- 이동 평균으로 데이터 대체
- 보간: 인접한 데이터를 기반으로 누락된 데이터를 추정해서 대입하는 방법
이전과 이후 데이터를 가지고 예측을 해서 설정 - 선형으로 예측
실제 작업을 할 때는 데이터의 분포를 확인을 해서 선형인지 비선형인지 결정
- DataFrame.interpolate 함수 이용
- quadratic: 비선형으로 채움 (값 기반), 기본은 선형으로 채움
- time: 시간 기반으로 채움
- limit_direction: 보간 방향 설정
# 결측치 채우기
time_index = pd.date_range("01/01/2024", periods=5, freq='M')
dataframe = pd.DataFrame(index = time_index)
#결측치를 포함하는 데이터를 생성
dataframe['Sales'] = [1, 4, 9, np.nan, 25 ]
dataframe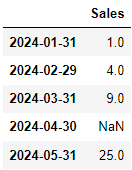 |
#결측치 앞값으로 채우기
dataframe.ffill()
#결측치 뒤값으로 채우기
dataframe.bfill()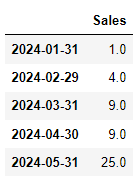  |
#선형으로 예측
dataframe.interpolate()
#비선형으로 예측
dataframe.interpolate(method="quadratic")  |
- 중간에 날짜가 비어 있는 경우에는 앞 뒤의 날짜를 확인해서
다음 날짜가 맞는지 아닌지 확인해서 값을 기반으로 할지 날짜를 기반으로 할지 결정
from datetime import datetime
dates = [datetime(2024, 1, 1),datetime(2024, 1, 2), datetime(2024, 1, 3),
datetime(2024, 1, 6), datetime(2024, 1, 7)]
dataframe = pd.DataFrame(index = dates)
dataframe['Sales'] = [1, 2, 3, np.nan, 7]
dataframe.interpolate(method='time')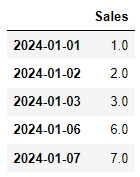 |
8-9) resampling
- 시계열의 빈도를 변환하는 것
- 다운 샘플링(데이터의 빈도를 줄이는 것 - 언더 샘플링)
- 원본 데이터의 시간 단위가 실용적이지 않은 경우: 어떤 것을 너무 자주 측정하는 경우
게시판의 글을 분석하기 위해서 로그 데이터를 읽을 때 시간 단위가 초까지 측정된 경우가 있다면 다운 샘플링을 고려 - 계절 주기의 특정 부분에 집중해야 하는 경우: 하나의 특정 계절에만 초점을 맞춘 분석을 해야 하는 경우
- 한 데이터를 낮은 빈도로 측정된 다른 데이터와 맞춰 주기 위해서
- 업 샘플링(데이터의 빈도를 늘리는 것 - 오버 샘플링)
- 시계열이 불규칙적인 경우
- 입력이 서로 다른 빈도로 샘플링된 상황에서 주기가 긴 데이터를 주기가 짧은 데이터에 맞추기 위해서
- resample(freq, how, fill_method, closed, label, kind)
- freq: 주기를 설정하는 것으로 이전에 사용하던 방식도 가능하고 '문자열단위', Hour, Minute, Second 등을 이용해서 설정하는 것도 가능(Second(30))
- how: 채우는 값으로 기본은 mean 이고 first, last, median, max, min 설정 가능
- fill_method: 업 샘플링을 할 때 데이터를 채우는 방법으로 기본은 None리고 ffill 이나 bfill 설정 가능
- limit: 채우는 개수
- closed: 다운 샘플링을 할 때 왼쪽 과 오른쪽 어떤 값을 사용할 지 여부를 설정
- label: 다운 샘플링을 할 때 왼쪽 과 오른쪽 어떤 인덱스를 사용할 지 여부를 설정
range = pd.date_range('2024-02-01', '2024-02-02', freq='2min')
#2분마다 20개 이므로 총 시간은 40분
df = pd.DataFrame(index=range)[:20]
df['price'] = np.random.randint(low=10, high=100, size=20)
df['amount'] = np.random.randint(low=1, high=5, size=20)
df |
#다운 샘플링 - 시간 간격을 10분으로 조정: 4개의 데이터로 변경
print(df.price.resample('10T').first())| 2024-02-01 00:00:00 71 2024-02-01 00:10:00 41 2024-02-01 00:20:00 69 2024-02-01 00:30:00 15 Freq: 10T, Name: price, dtype: int32 |
#시계열 데이터의 경우 시간별 집계를 수행하는 방법
print(df.price.resample('10T').sum())| 2024-02-01 00:00:00 360 2024-02-01 00:10:00 145 2024-02-01 00:20:00 267 2024-02-01 00:30:00 296 Freq: 10T, Name: price, dtype: int32 |
8-10) 이동 시간 윈도우
- 일반적인 기술 통계는 전체 데이터를 기반으로 계산하는데, 일정한 개수의 데이터를 가지고 움직이면서 기술 통계를 계산하는 것을 의미
-
- 단순이동평균
- 현재 위치에서 일정한 개수를 설정하고 그 이전 데이터와의 평균 계산
- DataFrame.rolling 함수 이용
- window: 데이터 개수 설정
- 지수이동평균
- 최근의 데이터에 가중치를 두는 방식
- 알파 = 1- span(기간)
- 현재데이터 + (1-알파)이전데이터 + (1-알파)제곱 * 이전에 이전 데이터... / 1 + (1-알파) + (1-알파)제곱..
- Dataframe.ewm 함수 이용
- span 옵션: span 설정
#2024년 1월 1일 부터 월 단위로 5개의 데이터를 생성
time_index = pd.date_range("01/01/2024", periods=5, freq='M')
#시계열 DataFrame을 생성
dataframe = pd.DataFrame(index=time_index)
dataframe['Stock_Price'] = [1, 2, 3, 4, 5]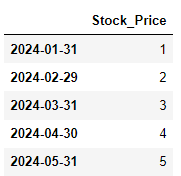 |
- pandas에서는 인덱스가 시간인 경우 또는 일정한 패턴인 경우를 시계열로 판정
#단순 이동 평균 계산
print(dataframe.rolling(window=2).mean())
#지수 이동 평균
print(dataframe.ewm(span=2).mean())| Stock_Price 2024-01-31 NaN 2024-02-29 1.5 2024-03-31 2.5 2024-04-30 3.5 2024-05-31 4.5 Stock_Price 2024-01-31 1.000000 2024-02-29 1.750000 2024-03-31 2.615385 2024-04-30 3.550000 2024-05-31 4.520661 |
8-11) 평활
- 시계열 자료의 체계적인 움직임을 찾아내기 위해서 과거 자료의 불규칙적인 변동 제거
- 불규칙 변동의 제거를 이동평균을 이용해서 분석
- 이동평균은 결국 과거 자료의 추세를 전 기간 또는 특정 기간 별로 평균을 계산해서 미래 자료를 예측한다는 것
- 과거 자료들의 가중치를 동일하게 적용하면 단순이동평균법, 각 자료의 가중치를 다르게 적용하면 지수평활법
8-12) 계절성 데이터
- 데이터의 계절성은 특정 행동의 빈도가 안정적으로 반복해서 나타나는 것으로 동시에 여러 빈도가 다르게 발생하는 것
- 시계열 데이터 중에는 일일, 주간, 연간의 계절적인 변화를 갖는 경향이 있는 데이터가 있음
- 그래프를 이용해서 대략적인 계절성 요인을 확인
- 계절성 시계열
- 일련의 동작이 정해진 기간동안 반복되는 시계열
- 주기가 일정
- 순환성 시계열
- 반복적인 동작이 있기는 하지만 기간이 일정하지않은 경우
- 주식 시작 이나 화산의 주기가 대표적인 순환성 시계열
- 계절성을 파악할 때는 산점도(scatter) 보다는 선(plot) 그래프를 이용하는 것이 좋다.

'Python' 카테고리의 다른 글
| [Python] 이미지 데이터 다루기 (0) | 2024.02.21 |
|---|---|
| [Python] 확률 (0) | 2024.02.21 |
| [Python] 데이터 전처리 (0) | 2024.02.15 |
| [Python] 데이터 시각화 (0) | 2024.02.14 |
| [Python] 데이터 탐색 (0) | 2024.02.14 |
