1. 분류
- 데이터를 가지고 어떤 결정을 해야 하는 문제를 접하는 경우, 결정해야 하는 Target이 이미 알려진 범주형일 때
이미 알려져있으므로 지도학습
- 분류의 유형은 이진분류(2가지 중 하나)와 다중분류(3가지 이상 중 하나)로 분류하기도 하고, 선형분류와 비선형분류와 나누기도 함
- sklearn의 분류기들은 예측하기 위한 함수로 2가지 사용
- predict: 분류 결과
- predict_proba: 각 클래스에 대한 확률(확률이 가장 높은 결과가 predict의 결과
1-1) 분류 알고리즘
- 판별 분석
- 랜덤 분류
- KNN
- Support Vector Machine
- 나이브 베이즈
- 로지스틱 회귀
- 결정 트리
- 최소 근접
- 신경망
- 앙상블
2. MNIST 데이터
- 0부터 9까지의 숫자 이미지 70,000개로 이루어진 데이터, 레이블이 존재
- sklearn을 이용해서 다운로드 받으면 data 속성에 피처가 존재하고 target 속성으로 레이블을 제공
1-1) MNIST 데이터 가져오기
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
X, y = mnist['data'], mnist['target']
print(X.shape)
print(y.shape)| (70000, 784) (70000,) |
- 이미지가 7만개 존재, 각 이미지에는 784개의 특성 존재
- 특성은 픽셀의 개수 (28x28)
#이미지 출력
#이미지 데이터 1개 가져오기
some_digit = X[0]
#이미지를 다시 2차원으로 변경
some_digit_image = some_digit.reshape(28, 28)
#출력
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
plt.axis('off')
plt.show() |
1-2) 훈련 데이터와 테스트 데이터 분리
print(y.dtype)| object |
- 정수로 형변환
#레이블 자료형을 정수로 변경
y = y.astype(np.uint8)| uint8 |
3. 이진 분류
3-1) 이진 분류를 위한 데이터 준비
- 타겟이 True 또는 False
- 이진 분류는 맞다 틀리다를 구분하는 것
- 레이블의 값을 True와 False로 생성
- 5가 맞는지 여부로 레이블 수정
# 이진 분류를 위한 레이블 생성
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
print(y_train_5[:10])
print(y_test_5[:10])| [ True False False False False False False False False False] [False False False False False False False False True False] |
3-2) sklearn.linear_model 의 SGDClassifier
- 확률적 경사 하강법 (Stochastic Gradient Descent - SGD) 사용하는 분류 모델 클래스
- 타겟을 찾아갈 때 한번에 찾아가지 않고 학습률 값을 이용해서 작게 분할해서 타겟을 찾아가는 방식
- 매우 큰 데이터 세트를 효율적으로 처리
- 한번에 하나씩 훈련 샘플을 독립적으로 처리하기 때문에 온라인 학습에 적합
- 온라인 학습: 실시간으로 데이터가 주어지는 형태의 학습 ↔ 배치 학습
- 하이퍼 파라미터
- max_iter: 최대 수행 횟수
- tol: 중지기준. 이 값보다 손실의 값이 작으면 훈련 중지 (어느정도까지 틀릴 것인지?)
- random_state
# SGDClassifier를 이용한 훈련
#모델 생성 및 학습
from sklearn.linear_model import SGDClassifier
#max_iter는 작업 횟수이고 tol은 중지 기준으로 loss가 tol 보다 작으면 훈련 중지 random_state는 seed 값
sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
#훈련
sgd_clf.fit(X_train, y_train_5) |
#첫 번째 데이터를 이용해 이미지 감지\
sgd_clf.predict([some_digit])| array([ True]) |
3-3) 분류의 평가 지표
- 오차 행렬: 정답이 True와 False로 나누어져 있고 분류 결과도 True와 False로 나누어서 표로 만든 형태
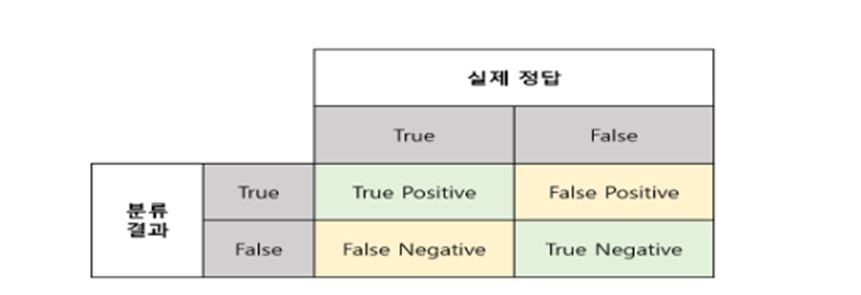
- True Positive(TP) : 실제 True인 정답을 True라고 예측 (정답)
- False Positive(FP) : 실제 False인 정답을 True라고 예측 (오답)
- False Negative(FN) : 실제 True인 정답을 False라고 예측 (오답)
- True Negative(TN) : 실제 False인 정답을 False라고 예측 (정답)
- confusion_matrix 함수를 이용해서 오차행렬 생성
- 타겟 클래스의 레이블과 예측 클래스의 레이블을 대입
- 예측 클래스의 레이블은 cross_val_predict(분류기, 피처, 레이블, cv=교차검증횟수) 호출
#이전 데이터와 분류기 이용해서 오차행렬 생성
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
#예측값 생성
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
#오차행렬 생성
confusion_matrix(y_train_5, y_train_pred)| array([[53892, 687], [ 1891, 3530]], dtype=int64) |
- 53892는 5가 아닌 것으로 제대로 분류
- 687는 5라고 잘못 분류한 것
- 1891은 5 이미지가 맞는데 5가 아니라고 분류한 개수
- 3550은 5라고 맞게 분류한 데이터
- Accuracy (정확도)
- True를 True로, False를 False로 예측한 비율
- 옳은 경우를 고려하는 지표

- 정확도는 가장 직관적으로 모델의 성능을 평가할 수 있는 지표
- 정확도를 사용할 때는 타겟의 비율을 확인해야 함
- 타겟의 비율이 어느정도 고르게 분포되어 있다면 고려할 수 있는 평가지표이지만,
타겟의 비율이 고르지 않다면 다른지표를 사용해야할 수 있다. - 어느 곳의 날씨가 99일은 맑고 1일은 비가 온다면, 무조건 맑다고 예측할 때 정확도가 99%가 된다.
- 타겟의 비율이 어느정도 고르게 분포되어 있다면 고려할 수 있는 평가지표이지만,
- Recall (재현율)
- True를 True라고 예측한 비율
- 실제 날씨가 맑은데 맑다고 예측한 비율
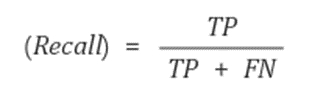
- sensitivity(민감도) 또는 hit rate 라고도 한다.
- Precision (정밀도)
- True라고 예측한 것 중에서 실제 True인 것의 비율
- 날씨가 맑다고 예측했는데 실제로 맑은 비율

- 정밀도와 재현율은 같이 사용하는 경우가 많다.
- F1 Score
- Precision과 Recall의 조화 평균
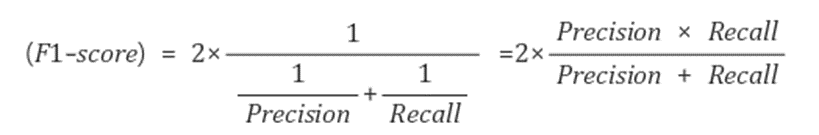
- Target의 비율이 불균형 구조일 때 모델의 성능 지표로 많이 이용
- sklearn.metrics에서 지표계산 API 제공
- 대입해야 하는 데이터: 실제 값과 예측한 값의 배열
- 보통의 경우 F1 Score가 좋으면 성능이 좋은 분류기라고 하지만, 상황에 따라서는 다른 지표 사용 고려
- 감시 카메라를 이용해서 도둑을 잡아내는 분류기를 훈련시킨다고 하면 정확도가 낮더라도 재현율이 좋은 것이 좋은 분류기가 될 수 있다.
- 어린 아이에게 동영상을 추천하는 시스템의 경우는 어린 아이에게 성인이 볼 영상을 추천하면 안됨
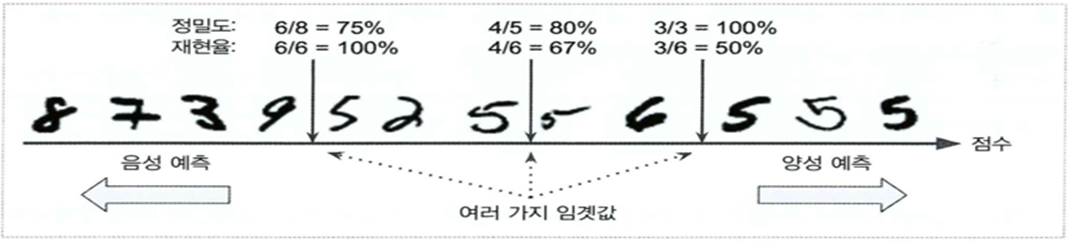
이런 경우에는 안전한 것들만 추천해줘야 하므로 정밀도가 높은 것이 좋은 분류기가 될 수 있다. - 일반적으로 정밀도를 올리면 재현율이 떨어지고, 재현율을 높이면 정밀도가 떨어진다.
이를 정밀도와 재현율의 트레이드 오프라고 한다.
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print("accuracy: %.2f" %accuracy_score(y_train_5, y_train_pred))
print("Precision : %.3f" % precision_score(y_train_5, y_train_pred))
print("Recall : %.3f" % recall_score(y_train_5, y_train_pred))
print("F1 : %.3f" % f1_score(y_train_5, y_train_pred))| accuracy: 0.96 Precision : 0.837 Recall : 0.651 F1 : 0.733 |
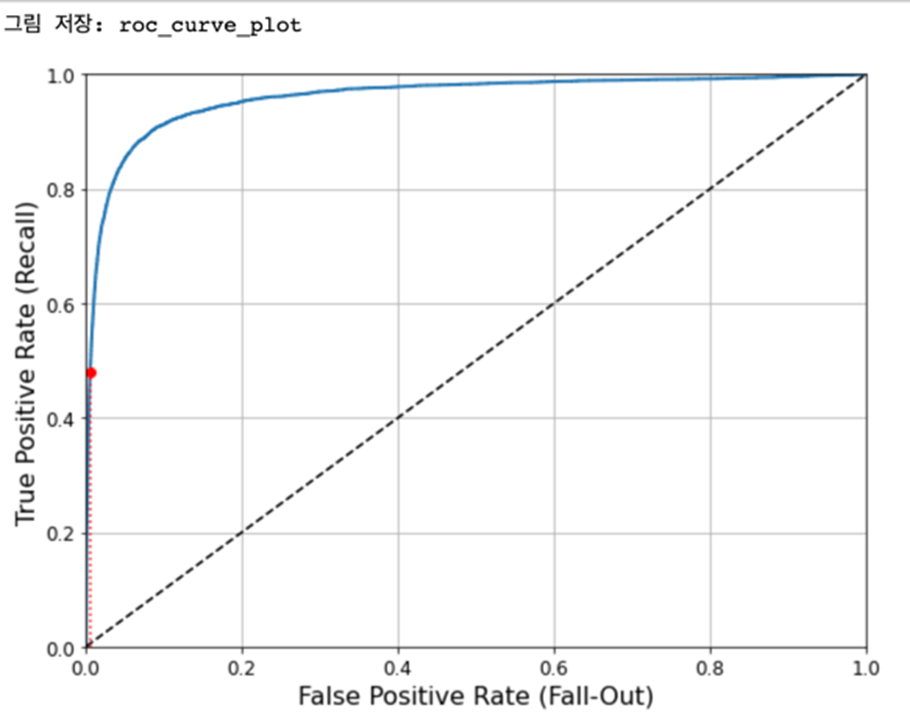
- ROC 곡선
- Receiver Operation Characteristic(ROC -수신기 조작 특성) 곡선도 이빈 분류에서 널리 사용되는 도구
- 거짓 양성 비율(False Positive Rate -FPR)에 대한 진짜 양성 비율(재현율)의 곡선
- 거짓 양성 비율은 양성으로 잘못 분류된 음성 샘플의 비율.
- 1 - 진짜 음성 비율 (음성으로 정확하게 분류한 음성 샘플의 비율) \
- 음성으로 정확하게 분류한 비율을 특이도(Specificity)라고 하는데 ROC 곡선은 재현율에 대한 1-특이도 그래프
- 이 값이 1에 가까우면 좋은 모델, 0.5에 가까우면 나쁜(랜덤) 모델
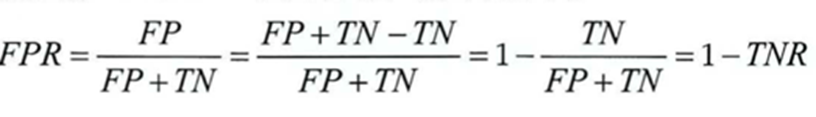
from sklearn.metrics import roc_auc_score
print('ROC_AUC:', roc_auc_score(y_train_5, y_train_pred))| ROC_AUC: 0.8192920558800075 |
3-4) RandomForestClassifier를 활용한 분류
- 예측하는 방법이 다른다. 이 클래스는 예측한 범주를 리턴하는게 아니라 predit_proba 함수를 이용해서 각 범주에 대한 확률값을 리턴
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5,
cv=3, method='predict_proba')
print(y_probas_forest([1]))| [0.99 0.01] |
- 훈련하고 예측하면 결과가 확률로 나온다.
#예측 - 양성 클래스의 확률
y_scores_forest = y_probas_forest[:, 1]
print(y_scores_forest[1])| 0.01 |
- y_scores_forest를 가지고 평가 지표를 구해야 함
print(roc_auc_score(y_train_5, y_scores_forest))| 0.9983436731328145 |
- RandomForest를 이용한 모델의 ROC 값이 이전 모델보다 높게 나옴
3-5) 교차 검증
- 여러 개의 fold로 나누어서 모델을 생성하고 훈련한 후 평가지표를 얻어서 평균을 구하기도 함
#교차 검증
from sklearn.model_selection import cross_val_score
#3번 수행해서 각 검증의 정확도 확인
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")| array([0.95, 0.96, 0.96]) |
#교차 검증
from sklearn.model_selection import cross_val_score
#3번 수행해서 각 검증의 정확도 확인
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")| array([0.95, 0.96, 0.96]) |
4. 다중 분류
- 둘 이상의 클래스를 구별하는 작업
- SGD, RandomForest, Naive Bayes 알고리즘은 여러개의 범주를 직접 처리할 수 있지만
- Logistic Regression, Support Vector Machine 같은 알고리즘은 이진분류만 가능
- 이진 분류기를 여러개 결합하면 다중 분류가 가능
4-1) 이진 분류 알고리즘을 이용한 다중 분류
- OvR(One-versus-the-Rest)
- 범주의 개수만큼 이진 분류기를 만들어서 가장 높은 결정 점수를 가진 분류기가 분류한 것을 선택
- 숫자분류기라면 숫자는 0부터 9까지 총 10개가 있으므로 분류기를 10개 만든다.
- 각 숫자에 해당하는 확률을 구해서 그 확률 중에서 가장 높은 것을 선택한다.
- OvO(One-versus-One)
- 두가지로 분류하는 이진분류기를 모두 (범주개수 * 범주개수-1) / 2 생성한 후 가장 많이 양성으로 분류된 범주를 선택
- 0/1, 0/2, 0/3, ... 8/9 구분까지 생성
- 그 중에서 가장 많이 분류된 클래스 선택
- sklearn에서는 다중 클래스 분류에 이진 분류 알고리즘을 사용하는 분류기를 선택하면 알아서 자동으로 알고리즘 선택
- 강제로 알고리즘을 선택할 수도 있다.
- SVM(Support Vector Machine)을 이용한 다중 분류
- SVM은 이진 분류기: 기본적으로 다중 분류를 하지 못함
- 이 분류기를 이용해서 다중 분류를 위한 데이터를 학습시키면 스스로 알고리즘을 선택해서 다중분류 결과 예측 가능
### 이진 분류기를 이용한 다중 분류
from sklearn.svm import SVC
#모델 생성
svm_clf = SVC(random_state=42)
#훈련
svm_clf.fit(X_train[:1000], y_train[:1000])
#예측
svm_clf.predict([some_digit])| array([5], dtype=uint8) |
some_digit = X[1]
svm_clf.predict([some_digit])| array([0], dtype=uint8) |
- 여러개의 분류기를 생성한 후 각각의 분류기를 가지고 예측을 해서 점수 배정
- 이 점수가 가장 높은 클래스 선택
some_digit = X[0]
some_digit_scores = svm_clf.decision_function([some_digit])
print(some_digit_scores)
some_digit = X[1]
some_digit_scores = svm_clf.decision_function([some_digit])
print(some_digit_scores)| [[ 1.758 2.75 6.138 8.285 -0.287 9.301 0.742 3.793 7.208 4.858]] [[ 9.305 -0.287 7.214 5.881 0.725 8.272 2.779 1.775 3.792 4.984]] |
- 이 점수나 확률은 확인할 필요가 있다.
- 5하고 제일 점수가 가까운 것은 8.285, [3]이다. 그러므로 5를 3으로 오분류할 가능성이 크다.
- 그래서 나중에는 오분류된 데이터만 가지고 다시 학습시키기도 한다.
- 강제로 알고리즘을 설정
#강제로 알고리즘 선택
from sklearn.multiclass import OneVsRestClassifier
ovr_clf = OneVsRestClassifier(SVC(random_state=42))
ovr_clf.fit(X_train[:1000], y_train[:1000])
some_digit = X[2]
print(ovr_clf.predict([some_digit]))| [4] |
4-2) 스케일링 적용 후 분류
#현재 데이터의 스케일링 상태 확인
print(X_train[0]) |
from sklearn.linear_model import SGDClassifier
#SGD 분류기 생성
sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
#훈련
sgd_clf.fit(X_train, y_train)
#교차 검증 수행
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")| array([0.874, 0.858, 0.869]) |
from sklearn.preprocessing import StandardScaler
#스케일을 해서 교차검증
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")| array([0.898, 0.891, 0.902]) |
-오차 행렬을 확인해서 어떤 부분에서 오류가 많이 발생하는지 확인
- 오류가 많이 발생하는 부분이 있다면 그에 해당하는 데이터를 더 수집해서 좀더 정확한 모델을 만드는 것을 고려하거나 이미지 데이터의 경우는 전처리를 수행해서 보정하기도 함
#오차 행렬
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx| array([[5577, 0, 22, 5, 8, 43, 36, 6, 225, 1], [ 0, 6400, 37, 24, 4, 44, 4, 7, 212, 10], [ 27, 27, 5220, 92, 73, 27, 67, 36, 378, 11], [ 22, 17, 117, 5227, 2, 203, 27, 40, 403, 73], [ 12, 14, 41, 9, 5182, 12, 34, 27, 347, 164], [ 27, 15, 30, 168, 53, 4444, 75, 14, 535, 60], [ 30, 15, 42, 3, 44, 97, 5552, 3, 131, 1], [ 21, 10, 51, 30, 49, 12, 3, 5684, 195, 210], [ 17, 63, 48, 86, 3, 126, 25, 10, 5429, 44], [ 25, 18, 30, 64, 118, 36, 1, 179, 371, 5107]], dtype=int64) |
5. 다중 레이블 분류
- 분류기가 샘플 별로 여러개의 결과를 출력하는 경우
- 이미지에서 객체를 탐지하는 경우 하나의 객체만 탐지하는 것이 아니고 여러개의 객체를 탐지해야 하는 경우나 얼굴에서 얼굴의 각 부위를 탐지하는 경우 등
#다중 레이블 생성
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
print(y_multilabel[0])| [False True] |
6. 판별 분석 (Discriminant Analysis)
- 2개 이상의 모집단에서 추출된 표본들이 지니고 있는 정보를 이용해서 이 표본들이 어느 모집단에서 추출된 것인지를 결정해줄 수 있는 기준을 찾는 분석
- 은행에서 부동산 담보 대출할 때 이 고객이 대출을 상환할 것인가 아니면 상환하지 않을 것인가를 판별하는 경우 은행에서는 기존의 대출을 상환하지 않은 고객들의 특성과 대출을 상환한 고객들의 특성을 별도로 만들어두고 이 고객의 특성이 어느쪽에 더 가까운건지 파악할 수 있다.
- 초창기에는 LDA(Linear Discriminant Analysis - 선형 판별 분석)를 많이 사용
- 최근에는 신경망 등이 등장하면서 사용빈도가 낮아졌다.
- 아직도 다른 머신러닝 알고리즘의 기반 알고리즘으로 사용됨
- 전체 표본의 크기가 독립 변수의 개수보다 3배 이상 많아야 함
6-1) LDA
- 내부 제곱합에 대한 사이 제곱합의 비율을 최대화하는 것이 목적
- 그룹 내부의 제곱합은 적게, 그룹과 그룹 사이의 제곱합은 크게 만드는 알고리즘
- 클러스터링의 기반이 되는 방법
- sklearn.discriminant.LinearDicriminantAnalysis 클래스 이용
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
#훈련할 때 여러개의 label인 묶인 타겟을 설정하면 다중 레이블 분류
knn_clf.fit(X_train, y_multilabel)
knn_clf.predict([some_digit])| array([[False, False]]) |
some_digit = X[0]
knn_clf.predict([some_digit])| array([[False, True]]) |
7. DummyClassifier
- 랜덤하게 분류
- 타겟의 비율을 보고 그대로 랜덤하게 예측하는 방식
8. KNN(K-Nearest Neighbor) 최근접 이웃
- 특징들이 가장 유사한 K개의 데이터를 찾아서 K개의 데이터를 가지고 다수결로 클래스를 선택해서 할당
- 회귀에 사용할 때는 그 값의 평균을 구해서 예측
8-1) 특징
- 간단: 전처리 과정에서 결측치를 대체하는 데 사용하기도 함
- 모델을 피팅하는 과정이 없음
- 모든 예측 변수들은 수치형이어야 함
- 거리를 계산해야 하기 때문
- 이 경우 범주형 데이터는 특별한 경우가 아니면 원핫 인코딩을 수행해야 함
- 게으른 알고리즘이라고 하는데 훈련 데이터 세트를 메모리에 전부 저장하고 거리 계산을 수행
- 온라인 처리가 안됨
8-2) API
- sklearn.neighbors.KNeighborsClassifier 클래스
- 인스턴스를 생성할 때 n_neighbors를 이용해서 이웃의 개수 설정
- metric을 이용해서 거리 계산 알고리즘을 설정하는데
1이면 맨하튼 거리, 2이면 유클리드 거리, 설정하지 않으면 mincowski 거리
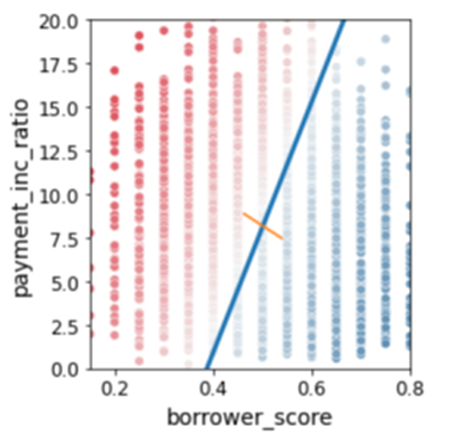
- 데이터: loan_200.csv
- payment_inc_ratio: 소득에 따른 대출 상환 비율
- dti: 소득에 대한 부채 비율
- outcome: 상환 여부
# KNeighborsClassifier를 이용해서 payment_inc_ratio와 dit에 따른 outcome 분류
#데이터 가져오기
loan200 = pd.read_csv('./python_machine_learning-main/data/loan200.csv') |
#데이터 분리
#테스트를 위한 데이터 1개 추출
newloan = loan200.loc[0:0, ['payment_inc_ratio', 'dti']]
#피처 추출
X = loan200.loc[1:, ['payment_inc_ratio', 'dti']]
#타겟 추출
y = loan200.loc[1:, 'outcome']
from sklearn.neighbors import KNeighborsClassifier
# 인스턴스 생성 - 필수적인 파라미터는 n_neighbors
# 모델 생성
knn = KNeighborsClassifier(n_neighbors=21)
#훈련
knn.fit(X, y) |
#예측
knn.predict(newloan)| array(['paid off'], dtype=object) |
#클래스별 예측 확률
print(knn.predict_proba(newloan))| [[0.476 0.524]] |
- predict 함수는 거의 모든 분류 모델이 소유하고 있지만
- predict_proba 함수는 없을 수 있다.
8-3) 거리 지표
- 유클리드 거리
- 서로의 차이에 대한 제곱합을 구한 뒤 그 값의 제곱근을 취하는 방식
- 유클리드 거리를 사용할 때는 수치형 데이터의 범위를 확인
- 맨하튼 거리
- 서로의 차이에 대한 절대값을 구한 뒤 모두 더한 거리
- 마할라노비스 거리
- 두 변수 간의 상관관계를 사용
- 유클리드 거리나 맨하튼 거리는 상관성을 고려하지 않기 때문에 상관관계가 있는 피처들의 거리를 크게 반영
- 주성분간의 유클리드 거리를 의미
- 많은 계산이 필요하고 복잡성이 증가
- 피처들의 상관관계가 높을 때 사용
- 민코프스키 거리
- 1차원 공간에서는 맨하튼 거리를 사용하고 2차원 공간에서는 유클리드 거리를 사용
8-4) 표준화
- 거리의 개념을 이용하므로 스케일링이나 표준화를 수행을 해주어야 함
- 표준화를 했을 때와 그렇지 않을 때 이웃이 달라지게 됨
- 10000 1 1 1 1
20000 1 1 1 1
11000 100 100 100 100
제곱을 하니까 단위 자체가 다름
8-5) 피처 엔지니어링
- KNN은 구현이 간단하고 직관적
- 성능은 다른 분류 알고리즘에 비해서 그렇게 우수한 편은 아니다.
- 다른분류 방법들의 특정 단계에 사용할 수 있게 모델에 지역적 정보를 추가하기 위해서 사용하는 경우가 많음
- 새로운 피처를 만드는 데 많이 사용
- 기존의 피처를 이용해서 새로운 피처를 만드는 것이라서 다중 공선성 문제를 야기할 것 같은데 KNN으로 만들어진 피처는 다중 공선성 문제가 거의 발생하지 않는다.
- KNN은 피처 전체를 이용하는 것이 주위 데이터 몇개만 이용하기 때문에 매우 지엽적인 정보 이용
- loan_data.csv.gz 데이터에서 새로운 피처 추가
- csv 파일의 크기가 너무 커지는 경우 파일을 gz 타입으로 압축해서 용량 줄일 수 있음
- pandas는 gz로 압축된 csv 파일의 내용을 읽을 수 있다.
- python은 zip이나 tar로 압축된 파일을 압축을 해제할 수 있고 여러 파일을 압축할 수 있는 API를 제공
# outcome 컬럼을 타겟으로 하고 나머지를 피처 특성으로 만들고, 피처 특성으로 타겟을 예측하도록 KNN으로 학습한 후 그 때의 예측 확률을 새로운 피처로 추가
loan_data = pd.read_csv('./python_machine_learning-main/data/loan_data.csv.gz') |
print(loan_data.info())
print(loan_data['outcome'].value_counts())| 15 outcome 45342 non-null object outcome default 22671 paid off 22671 Name: count, dtype: int64 |
- outcome은 카테고리인데, 자료형이 Object(문자열)
# 문자열을 범주형으로 전환
loan_data['outcome'] = pd.Categorical(loan_data['outcome'],
categories=['paid off', 'default'],
ordered=True)
loan_data.info()| 15 outcome 45342 non-null category |
#특성 행렬과 타겟 생성
X = loan_data[['dti', 'revol_bal', 'open_acc']]
y = loan_data['outcome']
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=20)
knn.fit(X, y) |
# knn으로 만들어진 예측 확률을 새로운 피처로 추가
# 예측 결과는 이차원 배열이므로 첫번째 열만 추가
loan_data['borrow_score'] = knn.predict_proba(X)[:, 0]
print(loan_data.info())
loan_data['borrow_score'].head()| 21 borrow_score 45342 non-null float64 0 0.50 1 0.40 2 0.40 3 0.55 4 0.55 Name: borrow_score, dtype: float64 |
- default, 빚을 갚지 않을 확률들!
예측 결과가 0이거나 1인 경우에는 1이 1일 확률만 내보낸다. 두번째 열은 없긴 함
그렇지만 머신러닝은 이차원 배열만 리턴한다. 하나의 데이터로만 예측하려 하진 않을테니까!
8-6) 특징
- 장점
- 이해하기 쉬운 모델
- 많이 조정하지 않아도 좋은 성능을 내는 경우가 있음
- 단점
- 예측이 느림
- 어떤 알고리즘이 특별히 있는게 아니라 예측할 데이터가 오면 그때 가서 이웃을 선정하고 예측함
- 많은 특성을 처리하는 능력이 부족
- 데이터를 전부 메모리에 로드해야하기 때문에 데이터가 많으면 사용하기 어려움 - 게으른 알고리즘
9. 나이브 베이즈
- 나이브 베이즈 알고리즘은 주어진 결과에 대해 예측 변수 값을 확률을 사용해서 예측 변수가 주어졌을 때 결과를 확률로 추정
- 완전한 또는 정확한 베이지언 분류 - 나이브 하지 않은 방식 (현실성이 없음)
- 예측 변수 프로파일이 동일한 모든 레코드를 찾음
- 해당 레코드가 가장 많이 속한 클래스(타겟값) 결정
- 새로운 레코드에 해당 클래스 지정
- 모든 예측 변수들이 동일하다면 같은 클래스에 할당될 가능성이 높기 때문에 예측 변수들이 같은 레코드를 찾는 데 무게를 두는 방식
- 나이브 베이즈
- 확률을 계산하기 위해 정확히 일치하는 레코드로만 제한하지 않고 전체 데이터 활용
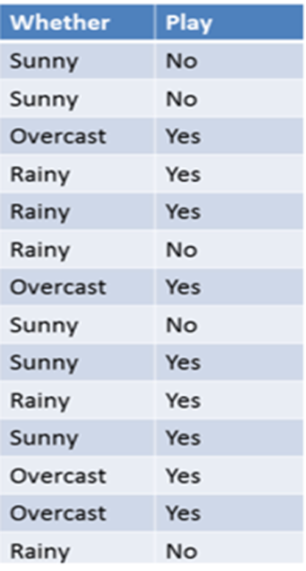
- overcast일 때 경기를 한 확률만이 아니라, 전체 날씨 중에 overcast인 확률도 넣었어야 한다.
-
단일 항목을 가지고 분류 - 날씨가 overcast일 때 경기를 할 확률은?P(Yes|Overcast) = P(Overcast|Yes) P(Yes) / P(Overcast)
- 사전 확률
P(Overcast) = 4/14 = 0.29
P(Yes) = 9/14 = 0.64 -
사후 확률
P(Overcast|Yes) = 4/9 = 0.44
- 베이즈 정리 공식에 대입
P(Yes|Overcast) = P(Overcast|Yes) P(Yes) / P(Overcast) = 0.44 * 0.64 / 0.29 = 0.98 - 결론: 날짜가 Overcast일 때 경기를 할 확률이 0.98이라는 의미
9-1) 나이브 베이즈 특징
- 일반적인 선형 분류기보다 훈련 속도가 빠른 편
- 일반화 성능은 일반적인 선형 분류기보다 떨어짐
- 효과적인 이유는 각 특성을 개별로 취급해서 파라미터를 학습하고 각 특성에서 클래스 별 통계를 단순하게 취합
- 텍스트 처리에서 주로 이용
9-2) API
- GaussianNB : 연속적인 데이터에 사용
- BernouliNB: 이진 데이터에 사용
- MultinomialNB: 카운트 데이터 (특성의 개수를 헤아린 정수값)
- BernouliNB와 MultinomialNB을 자연어 처리에 이용
loan_data = pd.read_csv('./python_machine_learning-main/data/loan_data.csv.gz')
loan_data['outcome'] = pd.Categorical(loan_data['outcome'],
categories=['paid off', 'default'],
ordered=True)
#purpose_, home_, emp_len은 범주형
loan_data['purpose_'] = loan_data['purpose_'].astype('category')
loan_data['home_'] = loan_data['home_'].astype('category')
loan_data['emp_len_'] = loan_data['emp_len_'].astype('category')- 타겟은 순서가 중요하다. 분류 할 때 각 타겟의 순서대로 확률을 제시하기 때문.
- 피처는 순서가 중요하지 않다. 바로 카테고리로 변환해도 된다. 나중에 원핫인코딩을 하기 때문.
#타겟과 피처 분리
predictors = ['purpose_', 'home_', 'emp_len_']
outcome = 'outcome'
#원핫 인코딩을 수행해서 특성 배열(피처 배열)을 생성
X = pd.get_dummies(loan_data[predictors], prefix='', prefix_sep='')
y = loan_data[outcome]
X.head() |
from sklearn.naive_bayes import MultinomialNB
naive_model = MultinomialNB()
naive_model.fit(X, y)
#146번 데이터 예측
new_loan=X.loc[146:146, :]
print("146번-", naive_model.predict(new_loan))
print(naive_model.classes_)
print("146번-", naive_model.predict_proba(new_loan))| 146번- ['default'] ['default' 'paid off'] 146번- [[0.65344472 0.34655528]] |
- default일 확률이 0.65, paid off일 확률이 0.34
print("146번-", naive_model.predict(new_loan)[0])| 146번- default |
10. Logistic Regression
- 타겟(종속변수)이 범주형인 경우 사용하는 회귀모형
- 분류만 가능
- 타겟이 2개 값을 갖는 경우에만 사용
- 피처의 자료형이 연속형에도 사용할 수 있고 이산형에도 사용 가능
10-1) Odds Ratio(특정 이벤트가 발생할 확률)
- Odds = 성공율 / 실패율 => 성공율 / (1-성공율)
- Odds Ratio = 한 그룹의 Odds / 다른 그룹의 Odds
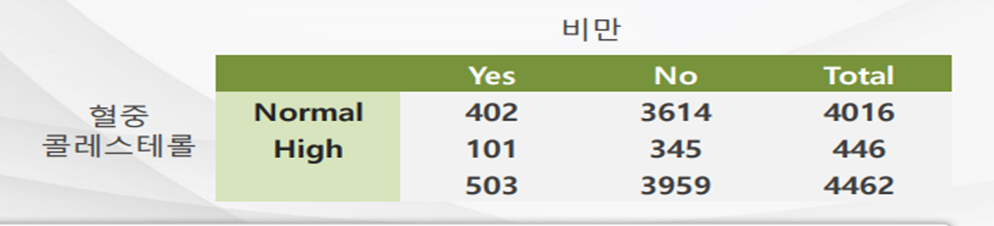
- 비만일 확률/(1-비만일 확률) =(402/4016)/(1-402/4016)) = 0.1001/0.8889 = 0.111
- 혈중 콜레스테롤이 정상인 그룹에서 비만이 아닌 경우의 오즈 0.899/0.1001 = 8.99
- Logit(P) = log(P/1-P)
- 값의 범위를 0- 1 범위로 입력받아서 자연 로그를 취한 함수가 Logit 함수
- P는 특성 x가 주어졌을 때 이 샘플이 클래스 1에 속할 조건부 확률
- 샘플이 특정 클래스에 속할 확률을 예측하는 것이 관심 대상이므로 logit 함수를 거꾸로 뒤집는데 이러한 함수가 로지스틱 시그모이드(logistic sigmoid function) 함수
- 약물 치료에 대한 환자의 반응(종속 변수)을 예측하고자 할 때 약물 치료 적용 후 환자가 살아남은 경우 1로 살아남지 못한 경우를 0으로 표현할 수 있음
| 단순선형회귀 | Logistic Regression 분석 |
 |  |
10-2) Logit 함수
- Odds Ratio에 로그를 취한 것
- 자연 로그를 취하면 부드러운 곡선의 형태
- 직선의 형태로 구분하는 단순 회귀보다는 조금 더 정확한 모델을 만들 가능성이 높다.
- 경계선 부분에 데이터가 많은 경우
10-3) API
- sklearn.linear_model LogisticRegression
- penalty : 페널티를 부여할 때 사용할 기준을 결정('l1', 'l2')
- dual : Dual Formulation인지 Primal Formulation인지를 결정(True, False)
- tol : 중지 기준에 대한 허용 오차 값
- C : 규칙의 강도의 역수 값
- fit_intercept : 의사 결정 기능에 상수를 추가할 지 여부 결정(True, False)
- class_weight : 클래스에 대한 가중치들의 값
- 타겟 값 비율이 다를 때
- random_state : 데이터를 섞을 때 사용하는 랜덤 번호 생성기의 시드 값
- solver : 최적화에 사용할 알고리즘 결정('newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga')
- max_iter : solver가 수렴하게 만드는 최대 반복 횟수 값
- multi_class : ('ovr', 'multinomial')
- warm_start : 이전 호출에 사용했던 solution을 재사용 할지 여부 결정(True, False)
- _jobs : 병렬 처리 시 사용 할 CPU 코어의 수
- n_jobs: n개만큼 동시에 작업, -1을 쓰면 최대만큼 묶어서 작업
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
print(X[:5])
print(iris.feature_names)
print(y[:5])
print(iris.target_names)| [[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2]] ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] [0 0 0 0 0] ['setosa' 'versicolor' 'virginica'] |
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)
print(log_reg.predict([X[0]])) #X[0]하나만 보더라도 [X[0]]| [0] |
print(log_reg.predict(X[0].reshape(-1, 4)))
print(y[0])| [0] 0 |
- 맞춤
print(X[0].reshape(-4, 1))| [[5.1] [3.5] [1.4] [0.2]] |
10-4) 소프트맥스 회귀
- 이진 분류 알고리즘을 가지고 다중 클래스 분류를 할 때는 여러 개의 분류를 만들어서 처리
- 클래스 개수만큼 이진 분류기를 만들어서 분류기를 통과한 결과 중 가장 높은 확률을 가진 클래스로 판정
- 2개씩 쌍으로 분류할 수 있는 모든 분류기를 만들어서 판정하는 방식
- 여러 개의 이진 분류기를 훈련시켜 연결하지 않고 직접 다중 클래스를 지원하도록 일반화한 방식 : 소프트맥스 회귀
- 소프트맥스 함수는 정규화된 지수함수라고도 하는데, 각 피처들을 가지고 클래스에 대한 점수를 계산하는 선형 회귀식을 만들어서 사용
- 각 클래스에 대한 선형 회귀식을 별도로 만들어 회귀식에 의해서 샘플에 대한 점수가 계산이 되면 소프트맥스 함수를 통과시켜서 확률 추정
10-5) 크로스 앤트로피
* 앤트로피: 불확실성. 값이 작을 수록 데이터가 잘 분리되어있다는 뜻.
- 모델에서 예측한 확률값이 실제값과 비교했을 때 틀릴 수 있는 정보량
- 값 이 적을 수록 모델이 데이터를 더 잘 예측하는 모델
- 정보 이론에서 유래
- 여러개의 상태가 있을 때 이 상태를 표현하는 방법을 비트 수를 다르게 해서 표현하는 방식
- 자주 등장하는 상태는 비트 수를 적게 해서 만들고 자주 등장하지 않는 상태는 비트 수를 크게 만드는 것
현재 상태가 4가지 (첫번째 상태가 90%이고, 나머지 상태가 7% , 2% , 1% 인 경우
- 일련번호 방식
- 00
- 01
- 10
- 11
- 원핫인코딩
- 1000
- 0100
- 0010
- 0001
- 크로스 앤트로피
- 0 - 첫번째 상태
- 10 - 두번째 상태
- 110 - 세번째 상태
- 1111 - 네번째 상태
10-6) 로지스틱 회귀에서 소프트맥스 사용법
- multi_class 옵션에 multinomial 적용
- solver 옵션에 lbfgs 같은 소프트맥스 알고리즘을 적용할 수 있는 알고리즘 설정
log_reg = LogisticRegression(multi_class = 'multinomial',
solver='lbfgs', random_state=42)
log_reg.fit(X, y)
print(log_reg.predict(X[0].reshape(-1, 4)))
print(y[0])
print(log_reg.predict(X[51].reshape(-1, 4)))
print(y[51])| [0] 0 [1] 1 |
11. SVM(Support Vector Machine)
- 일반적인 머신러닝 기법 중에서 매우 강력하고 선형 또는 비선형, 회귀, 이상치 탐색에도 사용하는 머신러닝 모델
- 초창기에는 가장 인기있는 모델에 속함, 현재는 아님
- 복잡한 분류 문제에 적합했고, 작거나 중간 크기의 데이터 세트에 적합
- 모든 속성을 활용하는 전역적 분류 모형
- 군집별로 초평면을 만드는데 이 초평면은 다른 초평면의 가장 가까운 자료까지의 거리가 가장 크게 만드는 것
11-1) 특징
- 장점
- 에러율이 낮음
- 결과를 해석하기 용이
- 단점
- 파라미터 및 커널 선택에 민감
- 이진분류만 가능
- 특성의 스케일에 굉장히 민감. 반드시 스케일링 수행해야 함
11-2) 하드마진과 소프트마진
- 하드마진
- 모든 데이터가 정확하게 올바르게 분류된 것
- 하드마진이 성립되려면 데이터가 선형적으로 구분될 수 있어야 하고, 이상치에 민감
- 소프트마진
- 이상치로 인해 발생하는 문제를 피하기 위해서 좀더 유연한 모델을 생성
- 어느정도의 오류를 감안하고 결정경계를 만들어내는 방식
- SVM에서 매개변수 C로 마진 오류 설정
- 마진 오류는 적은 것이 좋지만 너무 적게 설정하면 일반화가 잘 안됨
*일반화: 지금껏 보지 못한 데이터에 올바르게 적용되는 성질
- 마진 오류는 적은 것이 좋지만 너무 적게 설정하면 일반화가 잘 안됨
11-3) 선형 SVM 모델을 이용한 붓꽃 분류
- Pipeline을 사용
- 피처 스케일링과 모델 훈련을 하나의 파이프라인으로 묶어서 수행
#피처 스케일링
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
#모델 생성해서 훈련
from sklearn.svm import LinearSVC
svc_clf = LinearSVC(C=1, random_state=42)
svc_clf.fit(X, y)
#예측
svc_clf.predict([[5.5, 1.7]])| array([1.]) |
- 모든 컬럼에 스케일링하는 것이 동일하다면 파이프라인으로 묶는 것이 가능
#피처 스케일링
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
#스케일러와 분류기를 하나로 묶어서 사용
svm_clf = Pipeline([
('scaler', StandardScaler()),
('linear_SVC', LinearSVC(C=1, random_state=42))
])
svm_clf.fit(X, y)
svc_clf.predict([[5.5, 1.7]])| array([1.]) |
11-4) 비선형SVM
- 선형 SVM 분류기가 효율적이지만 선형적으로 분류할 수 없는 데이터가 많음
- 선형 SVM(커널)의 문제점중 하나가 XOR을 구분할 수 없는 점 => 다항식을 이용하여 해결
- 다항식을 이용하는 SVM을 생성하기 위해서는 PolynomialFeatures 변환기를 추가하면 됨
#데이터 생성
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.14, random_state=42)
#데이터 시각화
def plot_dataset(X, y, axes):
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.axis(axes)
plt.grid(True, which='both')
plt.xlabel("x_1", fontsize=20)
plt.ylabel("x_2", fontsize=20, rotation=0)
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5]) |
# 다항식을 추가한 선형 분류기
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=1,random_state=42))
])
polynomial_svm_clf.fit(X, y) |
| 다항식 없으면 | degree = 10 | degree = 30 |
 |  |  |
- degree는 추가되는 다항의 지수승을 의미한다.
- 숫자가 높아지면 잘 분류할 가능성은 높아지지만 학습할 피처의 개수가 늘어나고, 이로인해 훈련 속도도 느려지고 학습 속도가 느려진다.
- OVerfitting 될 가능성이 높아진다.
11-5) 다항식 커널
- 다항식 특성을 추가하면 성능이 좋아졌는데 낮은 차수의 다항식은 매우 복잡한 데이터 세트에는 잘 맞지 않을 것이고 높은 차수의 다항식은 굉장히 많은 특성을 추가하므로 모델을 느리게 함
- Kernel, Trick이라는 수학적 기교를 이용해서 실제로는 특성을 추가하지 않으면서 다항식 특성을 추가한 것과 같은 효과를 얻는 방법 사용
- 이 기법을 사용할 때는 SVC 클래스에서 매개변수 kernel에 poly 설정, 매개변수 degree에 적용하고자 하는 차수를 설정, 매개변수 coef()에 정수값을 설정. 낮은 차수와 높은 차수 중에서 어떤 다항식에 영향을 받을지 설정
#다항식 커널은 실제로 다항식을 추가하는 것이 아니라 추가하는 것과 같은 효과를 냄
from sklearn.svm import SVC
#스케일러와 분류기를 하나로 묶어서 사용
poly_kernel_svm_clf = Pipeline([
('scaler', StandardScaler()),
('svm_SVC', SVC(kernel='poly', degree=10, coef0=1, C=1, random_state=42))
])
poly_kernel_svm_clf.fit(X, y)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show() |
11-6) 유사도 특성을 추가하는 가우시안 RBF 커널
- 몇 개의 랜드마크를 추가한 후 이 랜드마크와의 유사도를 측정해서 그 값을 특성으로 추가
- SVC로 생성, 매개변수 kernel에 RBF, gamma 설정
- gamma를 너무 적은 수로 설정하면 선형 분류에 가까워지고 높게 설정하면 다항식을 이용하는 분류에 가까워짐
#가우시안 커널 이용
from sklearn.svm import SVC
rbf_kernel_svm_clf = Pipeline([
('scaler', StandardScaler()),
('svm_SVC', SVC(kernel='rbf', gamma=0.01, C=1, random_state=42))
])
rbf_kernel_svm_clf.fit(X, y)
plot_predictions(rbf_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show() |
11-7) 커널의 종류로 sigmoid도 존재
11-8) 시간복잡도
* 문자를 이용해서 행열을 표현할 때 앞의 숫자가 행의 수, 뒤의 숫자가 열의 수
- SGDClassifier(선형 회귀 분류): O(m*n)
- LinealSVC: O(m*n)
- SVC: O(m^ * n) ~ O(m^^ * n)
12. Decision Tree(결정 트리)
- 데이터 사이에 존재하는 패턴을 예측 가능한 트리 모양의 조건문 형태로 만드는 방식
- 복잡한 데이터세트도 학습하는 강력한 알고리즘
- RandomForest 모델의 기본 구성 요소
- 분류와 회귀에 모두 사용할 수 있고 다중 출력도 가능
- 분류에서는 마지막 터미널 값을 그대로 리턴하고 회귀의 경우는 평균을 리턴
- 트리는 한번 분기할 때마다 변수 영역을 2개로 구분
- 한번 구분한 뒤 순도가 증가하거나 불순도가 감소하는 방향으로 학습을 수행
- 순도가 증가하거나 불순도가 감소하는 것을 정보획득이라고 함
- API: DecisionTreeClassifer, DecisionTreeRegression
- max_depth: 트리의 깊이
iris = datasets.load_iris()
X = iris.data[:, 2:]
y = iris.target
from sklearn.tree import DecisionTreeClassifier
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
- leaf: (Terminal) 자식이 없는 노드
12-1) 트리 시각화를 위한 준비
- graphviz.org 다운로드, 환경변수에 path 추가
!pip install graphviz
!pip install pygraphvizfrom sklearn.tree import export_graphviz
import graphviz
export_graphviz(
tree_clf,
out_file="iris_tree.dot",
feature_names=iris.feature_names[2:],
class_names=iris.target_names,
rounded=True,
filled=True
)
with open('iris_tree.dot') as f:
dot_graph = f.read()
src = graphviz.Source(dot_graph)
src |
12-2) 트리 시각화
12-3) 불순도 지표
- 트리 모델은 순도가 증가하거나 불순도가 감소하는 방향으로 학습
- 지니계수(Gini Index): 오분류 오차
- 1에서 전체 데이터 개수에서 분류된 클래스의 데이터 개수를 제곱한 값을 전부 뺀 값
- 작은 값이 좋은 값
- 총 54개의 데이터를 분류했는데 클래스1이 0개, 클래스2가 49개, 클래스3이 5개로 분류된 경우
1 - (0/54)^ - (49/54)^ - (5/54)^
- 앤트로피
- 기본적으로는 지니 계수를 사용하지만 crieterion을 entropy로 설정하면 불순도 지표가 변경됨
- 하나의 영역에 2가지 클래스가 배정된 경우
하나의 영역에 16개의 데이터가 배정었고 1번이 10개, 2번이 6개가 배정되면
10/16 * log2(10/16) - 6/16 * log2(6/16) - 앞뒤 비율이 비슷해질수록 오분류 가능성이 커진다.
- 한쪽으로만 데이터가 배정되면 앞의 값이 0이 되고 뒤의 값도 0이 되어 결국 0이 됨.
0에 가까운 값이 좋은 값이다.
12-4) 규제 매개변수
- 결정 트리는 훈련 데이터에 대한 제약사항이 거의 없음
- 규제를 하지 않으면 트리가 훈련 데이터에 아주 가깝게 맞추려고 해서 과대적합이 발생
- 결정 트리는 모델의 하이퍼 파라미터가 없는 것이 아니라 훈련되기 전에 파라미터 수가 결정되지 않기 때문에 모델 구조가 데이터에 맞춰져서 고정되지 않고 자유로움
- 하이퍼 파라미터의 기본값이 대부분 Max 값이거나 None이다.
- 이전의 다른 모델은 하이퍼 파라미터의 값이 설정되어 있음
- 하이퍼 파라미터의 값이 기본값을 가지는 경우는 과대 적합될 가능성은 낮지만 과소 적합될 가능성이 있고 하이퍼 파라미터의 값이 기본값을 가지지 않고 MAX 값을 가지는 경우 과대 적합될 가능성은 높지만 과소 적합될 가능성은 낮다.
비선형 커널에서 degree라는 하이퍼 파라미터가 있다.
degree가 높으면 데이터를 정확하게 분류할 확률이 높다.
degree를 -1로 설정할 수 있다고 하면 정확하게 분류할 가능성은 높아지지만
- 결정 트리의 형태를 제한하는 매개변수
- max_depth: 최대 깊이, 특성의 개수를 확인해서 적절하게 설정
- min_samples_split: 분할을 할 때 가져야 하는 데이터의 최소 개수
- min_samples_leaf: 하나의 터미널이 가져야 하는 최소 개수
- min_weight_fraction_leaf: 개수가 아니라 비율로 설정
- max_leaf_nodes: 터미널의 개수
- max_features: 분할에 사용할 특성의 개수
min으로 시작하는 매개변수를 증가시키거나 max로 시작하는 매개변수를 감소시키면 규제가 커짐
- 규제가 커지면 오차가 발생할 확률은 높아진다.
12-5) 트리 모델의 단점
- 훈련 데이터의 작은 변화에도 매우 민감
- 조건문을 사용하는 방식이기 때문에 하나의 데이터가 추가되었는데 이 데이터가 조건에 맞지 않으면 트리를 처음부터 다시 만들어야 할 수도 있다.
- 트리 모델을 훈련시켜서 다른트리 모델과 비교하고자 할 때는 반드시 random_state를 고정시켜야 한다.
12-6) 피처의 중요도 확인
- 트리 모델에는 feature_importance
#피처의 중요도 확인
print(tree_clf.feature_importances_)
print(iris.feature_names[2:])| [0.56199095 0.43800905] ['petal length (cm)', 'petal width (cm)'] |
iris_importances_ = pd.Series(tree_clf.feature_importances_,
index=iris.feature_names[2:])
sns.barplot(x=iris_importances_, y= iris_importances_.index)
plt.show() |
12-7) 모델 생성 및 훈련
from sklearn.datasets import load_iris
#붓꽃 데이터 가져오기
iris = load_iris()
#피처 선택
#iris.data - 열의 개수가 4개인 2차원 배열
#iris.feature_names - 피처 이름 확인
#print(iris.feature_names)
#피처 선택
X = iris.data
#타켓 선택
y = iris.target
#결정 트리를 생성해서 훈련
from sklearn.tree import DecisionTreeClassifier
#max_depth 가 깊으면 정확한 분류를 해낼 가능성은 높지만 시간이 오래 걸리고
#과대 적합 문제 발생 가능성이 있음
#트리 모델은 트리를 한 개 생성하는 것이 아니고 여러 개 생성하므로
#각 트리가 동일한 데이터를 가지고 훈련해야 하므로 random_state를 고정시켜야 합니다.
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
12-8) 예측
#예측
result = tree_clf.predict([[5.1, 3.5, 1.4, 0.2]])
print(result)
12-9) 트리 모델 시각화
1) 트리 모델의 강점
- 화이트박스, 이해가 쉽다.
- 트리 구조 시각화
- 피처의 중요도 파악이 쉽다
- 별도의 파라미터 튜닝을 하지 않아도 좋은 성능
- 데이터 전처리가 거의 필요 없음
2) 시각화 준비
- graphviz 설치: 화면에 트리를 출력하는 것이 목적
- Windows
https://graphviz.org/download/#windows 에서 graphviz를 다운로드 받아서 설치
graphviz 가 설치된 디렉토리의 bin 디렉토리 와 bin 안에 있는 dot.exe 경로를 path에 추가
# 패키지 설치
pip install graphviz
- pygraphviz 설치: 출력된 트리를 이미지 파일로 만드는 것이 목적
- python -m pip install --use-pep517 --config-settings="--global-option=build_ext" --config-settings="--global-option=-IC:\Program Files\Graphviz\include" --config-settings="--global-option=-LC:\Program Files\Graphviz\lib" pygraphviz
\
3) 이미지로 출력
from sklearn.tree import export_graphviz
import graphviz
export_graphviz(
tree_clf,
out_file="iris_tree.dot",
feature_names = iris.feature_names,
class_names = iris.target_names,
rounded=True,
filled=True
)
#강제로 path 에 경로를 추가
import os
os.environ["PATH"] += os.pathsep + 'C:\Program Files\Graphviz\bin'
with open("iris_tree.dot") as f:
dot_graph = f.read()
src = graphviz.Source(dot_graph)
src
4) 이미지 파일로 저장
import pygraphviz as pga
from IPython.display import Image
graph = pga.AGraph("./iris_tree.dot")
graph.draw("iris_tree.png", prog='dot')
Image("iris_tree.png")
5) 최적의 파라미터 찾기 - 하이퍼 파라미터 튜닝( max_depth, min_sample_split)
from sklearn.model_selection import GridSearchCV
#파라미터 모음 만들기
params = {
'max_depth': [2, 4, 6, 8, 12, 16],
'min_samples_split': [2, 4, 8, 10]
}
grid_cv = GridSearchCV(tree_clf, param_grid=params, scoring='accuracy',
cv = 5, verbose=1)
grid_cv.fit(X, y)
print("가장 좋은 파라미터:", grid_cv.best_params_)
print("가장 좋은 정확도:", grid_cv.best_score_)
6) 피처의 중요도 확인
best_iris_clf = grid_cv.best_estimator_
iris_importances = pd.Series(best_iris_clf.feature_importances_,
index=iris.feature_names)
#2개의 피처는 영향력이 거의 없음
print(iris_importances)
iris_top3 = iris_importances.sort_values(ascending=False)[:3]
print(iris_top3)
sns.barplot(x=iris_top3, y=iris_top3.index)
plt.show()
'Python' 카테고리의 다른 글
| [Python] 머신러닝_앙상블 (0) | 2024.03.07 |
|---|---|
| [Python] 회귀 - 비선형 회귀 (0) | 2024.03.07 |
| [Python] 머신러닝 (0) | 2024.03.07 |
| [Python] 지도학습 연습 _ 자전거 대여 수요 예측 (0) | 2024.03.06 |
| [Python] 벡터 연산에서 기억할 부분 (0) | 2024.02.27 |
