1. 딥러닝
- 여러 비선형 변환 기법의 조합을 통해 높은 수준의 추상화를 시도하는 머신러닝 알고리즘의 집합
- 연속된 층(Layer)에서 점진적으로 의미있는 표현을 배우는 방식
- 기존의 머신러닝 방법은 1~2가지의 데이터 표현을 학습하는 얕은 학습을 수행하지만 딥러닝은 수백개 이상의 층 이용
- 데이터로부터 표현을 학습하는 수학 모델
- 층을 통과할 때마다 새로운 데이터 표현을 만들어가면서 학습
1-1) 작동 원리
- 층에서 입력 데이터가 처리되는 내용은 일련의 숫자로 이루어진 층의 가중치에 저장이 되는데 이는 그 층의 가중치를 parameter로 갖는 함수로 표현
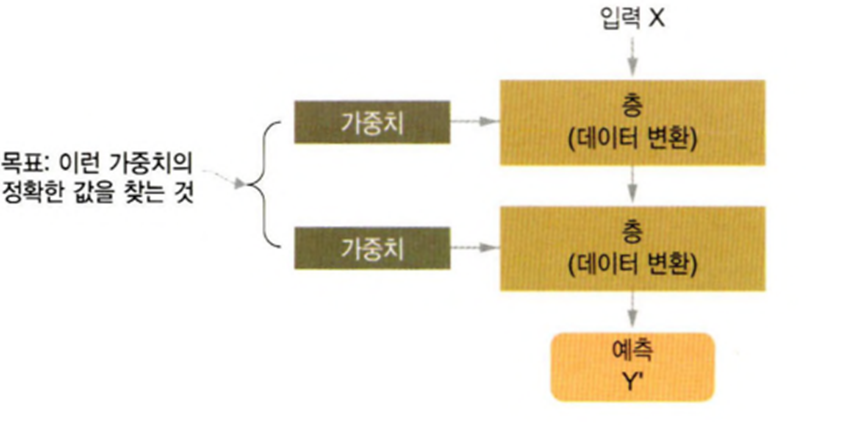
- 이 가중치를 알아내려면 데이터를 관찰해야 하고 신경망의 출력이 기대하는 것보다 얼마나 벗어났는지 측정
- 딥러닝은 기본적으로 지도학습
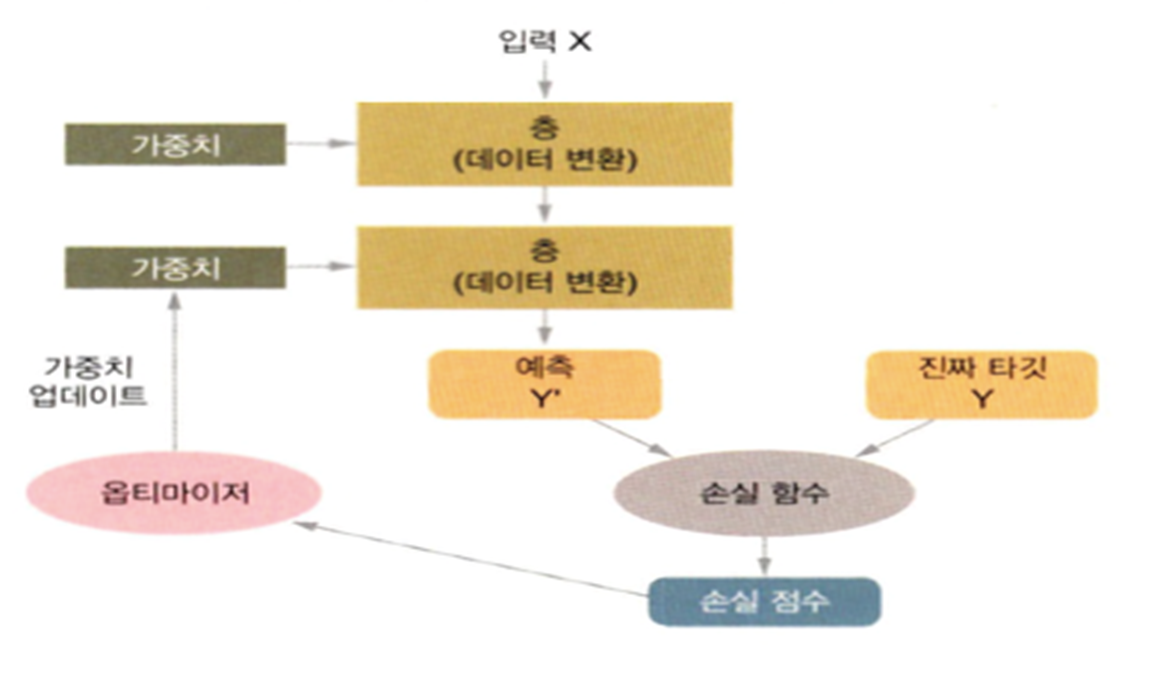
- 지도학습은 오차를 줄여나가는 작업이므로 오차를 측정하는 함수가 존재해야 하는데 이를 손실함수라고 한다.(Loss Function)
- 딥러닝은 손실 함수의 값이 감소하는 방향으로 가중치 값을 수정해나가는 것
- 초창기에는 네트워크의 가중치를 랜덤하게 할당하고 랜덤한 변환을 연속적으로 수행하는 방식을 사용했는데 이 방식은 수행을 많이 하게 되면 오히려 손실 점수가 높아지게 된다.
작동원리
1-2) 특징
- 딥러닝이 확산된 가장 큰 요인은 많은 문제에서 기존의 머신러닝 알고리즘보다 성능이 우수하기 때문
- 특성 공학을 완전히 자동화 함
- 기존의 머신러닝 알고리즘들은 대부분 알고리즘이 이해할 수 있도록 데이터를 변화하는 작업을 직접 수행
- 딥러닝은 데이터의 좋은 표현을 스스로 만들어낸다.
- 딥러닝이 학습할 때의 특징
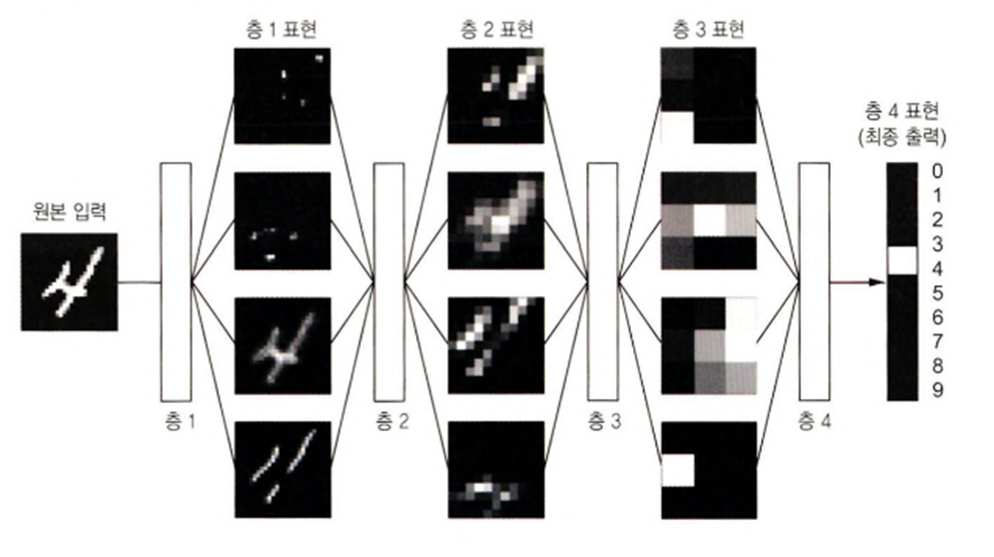
- 층을 거치면서 점진적으로 더 복잡한 표현을 만들어냄
- 점진적인 표현을 만드는 작업을 순차적으로 하는게 아니고 공동으로 학습
1-3) 최근 경향
- 2010년대 후반까지는 Kaggle에서 GBM과 Deep Learning을 사용한 모델이 우승을 차지했는데 GBM은 구조적인 데이터에 사용하고 Deep Learning은 이미지 분류와 지각에 관한 문제에 사용
- GBM 모델 중에서도 XGBoost가 주로 이용
- 패턴 인식 분야에서는 최근 거의 무조건 Deep Learning 사용
- 딥러닝을 많이 사용하게 된 이유는 하드웨어의 발전과 데이터의 증가
1-4) 장점
- 성능이 우수
- 특성 공학이 자동
- 구조화되지 않은 데이터 학습 능력이 뛰어남
1-5) 제한
- 학습 데이터가 많아야 함
- 네트워크가 만들어 낸 특성을 해석하기가 어려움
- 컴퓨팅 자원이 많이 필요
- 데이터의 크기가 기가 바이트를 넘지 않는다면 딥러닝과 머신러닝은 별 차이가 없다.
1-6) 딥러닝 패키지
- Torch
- C로 구현된 라이브러리로 페이스북에서 Torch로 만들 PyTorch를 내놓으면서 유명
- 연구용으로 많이 사용
- Theano
- Numpy 배열과 관련성이 높은 패키지로 계산을 많이 하는 연구에 이용
- 구글의 오픈소스인 Tensorflow가 Theano에서 영감을 얻은 라이브러리
- 프로덕션 구현이 강력 - PC, Android, Web용 라이브러리 제공
- CuDNN
- CUDA Deep Neural Network의 약자로 GPU 구현을 위한 라이브러리 제공
2. 인공 신경망 (ANN - Artificial Neural Network)
- 근원: 지능적인 기계를 만드는 법에 대한 영감을 얻으려면 뇌 구조를 살펴보는 것이 합리적이라고 판단
- 인공 신경망은 뇌에 있는 생물학적 뉴런의 네트워크에서 영감을 받은 머신러닝 모델이지만 새를 보고 비행기에 대한 영감을 얻었다고 해서 비행기 날개를 새처럼 펄럭 거릴 필요는 없는데 인공 신경망도 생물학적 뉴런에서 점점멀어지고 있음
- 일부에서는 neuron이라는 표현 대신에 unit이라고 지칭
- 1943년에 워런 매컬러의 논문에서 처음 소개
2-1) 뉴런을 이용한 논리 연산
- 가장 처음 만든 모델은 하나 이상의 이진 입력과 이진 출력 하나를 가짐
- 이 모델을 가지고 not, or, and 연산 수행
2-2) Perceptron
- 입력과 출력이 이진이 아닌 숫자이고 각각의 입력 연결은 가중치와 연관되어 있음
- 입력의 가중치 합을 계산한 뒤 계산된 합에 함수(계단 함수 - step function)를 적용해서 결과를 출력
- 가장 많이 사용되는 계단 함수: heaviside와 sign function
- heaviside는 가중치의 합이 0보다 작으면 0, 0보다 크거나 같으면 1을 리턴하는 함수
- sign function은 가중치의 합이 0보다 작을 때 -1, 0일 때 0, 0보다 클 때 1을 리턴하는 함수
- 이러한 perceptron이 여러개 모여서 하나의 Layer를 구성하게 되고 이전 층의 모든 뉴런과 연결된 것을 Fully Connected Layer(완전연결층) 또는 Dense Layer(밀집층)
- 입력은 입력 뉴런이라고 하는 특별한 뉴런에 주입이 되는데 이러한 입력 뉴런으로 구성된 레이러를 Input Layer라고 부른다.
- 이 레이어가 다른 점은 편향 특성이 더해지는데 (x0 = 1) 이 편향 특성은 항상 1을 출력하는 특별한 종류의 뉴런이라고 해서 편향 뉴런(Bias Neuron)이라고 표현
- Perceptron은 선형 분류 모형의 형태를 갖게 됨
- 논리 연산 중 XOR 문제를 해결하지 못함
2-3) MLP
- Perceptron이 지닌 한계점을 극복하기 위해서 여러개의 Layer를 쌓아 올린 MLP(Multi Layer Perceptron)이 등장
- Perceptron은 기본적으로 Input과 Output Layer로만 구성되지만 MLP는 이 중간에 Hidden Layer를 추가한 형태
- Hidden Layer는 여러개의 Perceptron이 모여있는 구조
- Hidden Layer를 여러개 쌓으면 깊어지기 때문에 이를 Deep Learning이라고 부름
- Input에서 Weight을 계산하고 Hidden Layer를 거쳐서 Output을 만들어내는데 이 과정을 Feed Forward라고 한다.
2-4) Activation Function
- 어떤 신호를 받아서 이를 적절히 처리해서 출력해주는 함수
- Input과 Weight를 받아서 연산을 수행해주는 함수
- 신경망은 비선형 Activation Function을 선호
- 선형 함수: Sign Function, Heaviside Step
- Sigmoid(로그함수 - 1/(1 + e의 -x승))
- Sigmoid 함수는 입력 값이 0 이하이면 0.5 이하의 값을 출력하고 0 이상이면 0.5 이상의 값을 출력하는데 입력 값에 대해서 0과 1 사이의 값으로 Scailing 해주는 개념의 함수
- Sign Function과 Heaviside는 선형이고 Sigmoid는 비선형
- 대부분의 경우 비선형이 선형보다 우수한 성능을 발휘하기 때문에 신경망은 비선형을 선호
- Sigmoid 함수는 복잡한 문제를 해결할 수는 있지만 Back Propagation 과정 중 Gradient Vanishing(소멸) 현상이 발생할 수 있음
- 모델이 깊어질수록 이러한 현상이 자주 발생
- softmax 함수
- Sigmoid를 일반화시킨 함수로 다중 클래스 분류에 가장 적합
- ReLU (Rectified Linear Unit)
- 전체 입력이 0보다 크면 출력은 순입력(가중치를 곱하고 편향을 더한 값)과 같고 전체 입력이 0보다 작거나 같으면 0을 출력
- y = max(0, 가중치*입력 + 편향)
- ReLU는 입력이 양수이고 기울기가 0이어도 일정한 기울기를 가지게 됨
- 양수만 보면 선형이지만 0이나 0보다 작을 때 0의 값을 갖도록 해서 비선형을 만들어 냄
- 음수일 때도 기울기를 가지도록 만들어진 함수가 있는데 이 함수는 PReLU
- Hyperbolic Tangent : tanh
- 출력이 0인 지점에서 기울기를 가짐
2-5) Learning Rate 학습률
- 경사 하강법에서 가중치를 업데이트 할 때 간격
- 숫자가 커지면 최적의 지점을 찾지 할 수 있고 너무 작은 값을 선택하면 학습 속도가 느려질 수 있음
- 신경망에서는 0.01 아래의 값을 사용하는 것을 권장
2-6) Back Propagation 역전파
- Input 에서 Output 까지 계산을 수행하고 그 결과와 실제 답과의 오차를 구해서 오차가 작아지는 형태로 가중치를 조정해야 하는데, 가중치를 조정할 때 뒤에 있는 가중치를 먼저 업데이트 한다고 해서 역전파 알고리즘이라고 부름
- 한번 Feed Forward 로 작업을 수행하고 Back Propagation을 수행하면 1번의 epoch 라고 함
- 알고리즘을 수행할 때 모든 데이터를 가지고 한꺼번에 하지는 않고 일반적으로 mini batch 라고 부르는 작은 단위로 실행
3. TensorFlow
- 구글이 만든 Deep Learning에 초점을 맞춘 라이브러리
- GPU 지원
- 분산 컴퓨팅을 지원: 여러 대의 컴퓨터에서 동시에 학습 가능하고 예측도 가능
- 플랫폼에 중립적인 포맷으로 내보낼 수 있음
- 리눅스를 사용하는 파이썬 환경에서 Tensorflow 모델을 훈련시키고 이 모델을 안드로이드에서 실행할 수 있음
3-1) API
- 거의 모든 운영체제를 지원하고 Tensorflow Lite를 이용하면 안드로이드 와 iOS 같은 모바일 운영체제에서도 실행되고 Python API를 많이 이용하지만 C++, Java, Go(golang), Swift API도 제공됨
- Tensorflow Hub에서 사전에 훈련된 신경망을 쉽게 다운로드 받아서 사용할 수 있음
- https://www.tensorflow.org/resources
3-2) 연산
- 가장 저 수준의 연산은 C++ 코드로 만들어져 있음
- 연산들이 여러 종류의 커널에서 수행: CPU, GPU, TPU 등
- TPU는 Deep Learning 연산을 위해 특별하게 설계된 ASIC Chip
3-3) 설치
pip install tensorflow- numpy 버전과 tensorflow 버전이 서로 충돌할 때가 있다.
버전확인
import tensorflow as tf
print(tf.__version__)
4. Tensorflow 사용
4-1) Tensor 생성
- numpy의 ndarray와 유사한 방식으로 생성
- immutable 데이터(변경 불가)는 tf.constant로 생성
tf.constant(42) # 스칼라
tf.constant([[1., 2., 3.], [4., 5., 6.]]) # 행렬
t = tf.constant([[1., 2., 3.], [4., 5., 6.]])
t| <tf.Tensor: shape=(2, 3), dtype=float32, numpy= array([[1., 2., 3.], [4., 5., 6.]], dtype=float32)> |
print(t[:, 1]) #1번째 열: 하나의 열이라서 1차원 배열
print()
print(t[:, 1:]) #1번째 열부터 모든 열
print()
print(t[..., 1, tf.newaxis])| tf.Tensor([2. 5.], shape=(2,), dtype=float32) tf.Tensor( [[2. 3.] [5. 6.]], shape=(2, 2), dtype=float32) tf.Tensor( [[2.] [5.]], shape=(2, 1), dtype=float32) |
- 1차원 배열이 2차원 배열이 된다.
4-2) 연산
- numpy 의 ndarray 와 거의 동일한 방식으로 연산을 수행하고 함수 나 메서드의 이름도 거의 일치
print(t + 10)
print()
print(tf.square(t))
print()
print(t @ tf.transpose(t))| tf.Tensor( [[11. 12. 13.] [14. 15. 16.]], shape=(2, 3), dtype=float32) tf.Tensor( [[ 1. 4. 9.] [16. 25. 36.]], shape=(2, 3), dtype=float32) tf.Tensor( [[14. 32.] [32. 77.]], shape=(2, 2), dtype=float32) |
- tensorflow나 numpy에서 배열을 가지고 산술연산을 하는 경우 실제로는 함수 호출
- python 에서는 __이름__ 형태로 메서드를 만드는 경우가 있는데 이러한 함수들은 Magic Function 이라고 부르는데 사용을 할 때 메서드 이름을 호출하는 것이 아니라 다른 연산자를 이용한다.
- 이렇게 연산자의 기능을 변경하는 것을 연산자 오버로딩
- 객체 지향에서만 가능합니다.
- + 는 숫자 두 개를 더하는 기능을 가지고 있는데 tensorflow 나 numpy 에서는 __add__를 정의해서 이 메서드를 호출하도록 한다.
- 이름이 다른 함수도 있음
- np.mean -> tf.reduce_mean
- tf.float32 는 제한된 정밀도를 갖기 때문에 연산을 할 때 마다 결과가 달라질 수 있음
- 동일한 기능을 하는 함수나 클래스를 Keras 가 별도로 소유하고 있는 경우도 있음
- Keras는 Tensorflow 의 저수준 API(Core 에 가까운 쪽)
4-3) Tensor와 numpy의 ndarray
- 2개의 데이터 타입은 호환이 되서 서로 변경이 가능
- Tensor를 ndarray 로 변환하고자 하는 경우는 numpy() 메서드를 호출해도 되고 numpy 의 array 함수에 Tensor를 대입해도 된다.
- ndarray를 가지고 Tensor를 만들고자 할 때는 contant 나 variable 같은 함수에 대입
ar = np.array([2, 3, 4])
print(tf.constant(ar))| tf.Tensor([2 3 4], shape=(3,), dtype=int32) |
ar = np.array([2, 3, 4])
print(tf.constant(ar))| [2 3 4] [2 3 4] |
4-4) 타입 변환
- Data Type이 성능을 크게 감소시킬 수 있음
- Tensorflow 는 타입을 절대로 자동 변환하지 않는다.
- 데이터 타입이 다르면 연산이 수행되지 않음
- 타입이 다른데 연산을 수행하고자 하는 경우에는 tf.cast 함수를 이용해서 자료형을 변경해야 함
- Tensorflow 가 형 변환을 자동으로 하지 않는 이유는 사용자가 알지 못하는 작업은 수행을 하면 안된다는 원칙 때문
#ndarray는 이렇게 자료형이 다른 경우 자동으로 자료형을 변경해서 연산을 수행
print(np.array([1, 2, 3]) + np.array([1.6, 2.3, 3.4]))| [2.6 4.3 6.4] |
#자료형이 달라서 에러가 발생
print(tf.constant(2.0) + tf.constant(40))| InvalidArgumentError: cannot compute AddV2 as input #1(zero-based) was expected to be a float tensor but is a int32 tensor [Op:AddV2] name: |
t1 = tf.constant(40)
#형 변환 한 후 연산 수행
print(tf.constant(2.0) + tf.cast(t1, tf.float32))| tf.Tensor(42.0, shape=(), dtype=float32) |
4-5) 변수
- 일반적인 데이터는 직접 변경을 하지 않기 때문에 constant 로 생성해서 사용하면 되는데 역전파 알고리즘을 수행하게 되면 가중치가 업데이트된다고 했는데 가중치는 수정되어야 하기 때문에 constant로 생성되면 안됨
- 수정되어야 하는 데이터는 tf.Variable 을 이용해서 생성
- 데이터를 수정하고자 하는 경우는 assign 함수를 이용
- assign_add 나 assign _sub를 이용해서 일정한 값을 더하거나 빼서 수정할 수 있음
- 배열의 일부분을 수정할 때는 assign 함수나 scatter_update() 나 scatter_nd_update ()를 이용
#변수 생성
v = tf.Variable([[1, 2, 3], [4, 5, 6]])
print(v)
print(id(v))
#이 경우는 데이터를 수정한 것이 아니고
#기존 데이터를 복제해서 연산을 수행한 후 그 결과를 가리키도록 한 것
#참조하는 위치가 변경됨
v = v * 2
print(v)
print(id(v))
#내부 데이터 수정
v = tf.Variable([[1, 2, 3], [4, 5, 6]])
print(v)
print(id(v))
#이 경우는 id 변경없이 데이터를 수정
v.assign(2 * v)
print(v)
print(id(v))| <tf.Variable 'Variable:0' shape=(2, 3) dtype=int32, numpy= array([[1, 2, 3], [4, 5, 6]])> 2832592070160 tf.Tensor( [[ 2 4 6] [ 8 10 12]], shape=(2, 3), dtype=int32) 2832590246432 <tf.Variable 'Variable:0' shape=(2, 3) dtype=int32, numpy= array([[1, 2, 3], [4, 5, 6]])> 2832592070992 <tf.Variable 'Variable:0' shape=(2, 3) dtype=int32, numpy= array([[ 2, 4, 6], [ 8, 10, 12]])> 2832592070992 |
4-6) Data구조
- 종류
- SparseTensor: 0이 많은 Tensor를 효율적으로 나타내는데 tf.sparse 패키지에서 이 Tensor에 대한 연산을 제공
- TensorArray: Tensor의 list
- RaggedTensor: list 의 list
- stringtensor: 문자열 텐서인데 실제로는 바이트 문자열로 저장됨
- set
- queue
4-7) Tensorflow 함수
- 일반 함수는 python 의 연산 방식에 따라 동작하지만 Tensorflow 함수를 만들게 되면 Tensorflow 프레임워크가 자신의 연산 방식으로 변경해서 수행을 하기 때문에 속도가 빨라질 가능성이 높음
- 생성방법
- 함수를 정의한 후 tf.function 이라는 decorator를 추가해도 되고 tf.function 함수에 함수를 대입해서 리턴받아도 됨
- 함수를 변경하는 과정에서 Tensorflow 함수로 변경이 불가능하면 일반 함수로 변환
4-8) 난수 생성
- tf.random 모듈을 이용해서 난수를 생성
5. 뉴런 생성
- 뉴런을 추상화하면 Perceptron
5-1) 입력 -> 뉴런 -> 출력
- 이런 여러 개의 뉴런이 모이면 Layer 라고 하며 이런 Layer의 집합이 신경망
5-2) 뉴런의 구성
- 입력, 가중치, 활성화 함수, 출력으로 구성
- 입력과 가중치와 출력은 일반적으로 정수나 실수
- 활성화 함수는 뉴런의 출력 값을 정하는 함수
- 간단한 형태의 뉴런은 입력에 가중치를 곱한 뒤 활성화 함수를 취하면 출력을 얻어 낼 수 있음
- 뉴런은 가중치를 처음에는 랜덤하게 초기화를 해서 시작하고 학습 과정에서 점차 일정한 값으로 수렴
- 학습 할 때 변하는 것은 가중치
- 활성화 함수는 시그모이드나 ReLU 를 주로 이용
- 최근에는 주로 ReLU를 주로 이용
- 뉴런을 직접 생성
#시그모이드 함수
import math
def sigmoid(x):
return 1 / (1 + math.exp(-x))
#입력
x = 1
#출력
y = 0
#한번 학습
w = tf.random.normal([1], 0, 1) #가중치
output = sigmoid(x * w)
print(output)| 0.5174928205334988 |
#학습률을 0.01 로 설정해서 경사하강법을 수행
#학습 횟수 - epoch
for i in range(1000):
#출력을 생성
output = sigmoid(x * w)
#출력 오차를 계산
error = y - output
#가중치 업데이트
w = w + x * 0.1 * error
#횟수 와 오차 그리고 출력값을 확인
if i % 100 == 0:
print(i, error, output)| 0 -0.000905242523688215 0.000905242523688215 100 -0.0008971286421305708 0.0008971286421305708 200 -0.0008891556201675512 0.0008891556201675512 300 -0.0008813285493673459 0.0008813285493673459 400 -0.0008736348299158559 0.0008736348299158559 500 -0.0008660738198464301 0.0008660738198464301 600 -0.0008586448693105883 0.0008586448693105883 700 -0.000851337993012676 0.000851337993012676 800 -0.0008441600044856342 0.0008441600044856342 900 -0.0008370967242979266 0.0008370967242979266 |
- 입력 데이터가 0 이고 가중치를 업데이트하는 식이 w + x * 0.1 * error 라서 x 가 0이 되면 가중치를 업데이트 할 수 없음
- 단순하게 시그모이드 함수를 적용하면 이 경우 최적점에 도달할 수 없고 계속 0.5 만 출력
- 입력 데이터 0에서 기울기가 없어지는 현상 - 기울기 소실 문제(Gradient Vanishing)
- 이 경우에는 시그모이드 함수 대신에 0에서 기울기를 갖는 ReLU를 사용하거나 시그모이드 함수에 데이터를 대입할 때 편향을 추가해서 해결
#입력
x = 0
#출력
y = 1
#학습률을 0.01 로 설정해서 경사하강법을 수행
#학습 횟수 - epoch
for i in range(1000):
#출력을 생성
output = sigmoid(x * w)
#출력 오차를 계산
error = y - output
#가중치 업데이트
w = w + x * 0.1 * error
#횟수 와 오차 그리고 출력값을 확인
if i % 100 == 0:
print(i, error, output)| 0 0.5 0.5 100 0.5 0.5 200 0.5 0.5 300 0.5 0.5 400 0.5 0.5 500 0.5 0.5 600 0.5 0.5 700 0.5 0.5 800 0.5 0.5 900 0.5 0.5 |
5-3) AND를 구현
- AND 연산
0 0 -> 0
0 1 -> 0
1 0 -> 0
1 1 -> 1
- 입력 피처는 2개이고 출력은 1개, 가중치는 2개가 되어야 한다.
가중치는 입력 피처마다 설정됨
#입력과 출력 데이터 생성
X = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([[0], [0], [0], [1]])
#가중치 초기화
w = tf.random.normal([2], 0, 1) #입력 피처가 2개이므로 가중치도 2개
b = tf.random.normal([1], 0, 1) #편향
#학습
for i in range(3000):
#샘플이 여러 개이므로 에러는 모든 샘플의 에러 합계로 계산
#에러 합계를 저장할 변수
error_sum = 0
#4는 입력 데이터의 개수
for j in range(4):
#출력
output = sigmoid(np.sum(X[j] * w)+ 1*b)
#오차
error = y[j][0] - output
#가중치 업데이트 - 학습률은 0.1
w = w + X[j] * 0.1 * error
#편향 업데이트
b = b + 1 * 0.1 * error
#에러 값을 추가
error_sum += error
#100번 훈련을 할 때 마다 에러의 합계를 출력
if i % 100 == 99:
print(i, error_sum)| 99 -0.17735192112485976 199 -0.11300731067658454 299 -0.08377195476035765 399 -0.06660772360599848 499 -0.05523404708400695 599 -0.047131021104291515 699 -0.0410676336021214 799 -0.036362474376702675 899 -0.03260789231152378 999 -0.02954500410502825 1099 -0.026999358822200475 1199 -0.024851178654502953 1299 -0.023015025341699566 1399 -0.02142777432262047 1499 -0.020043216619398396 1599 -0.018823937643251798 1699 -0.017743068185467267 1799 -0.01677645680136907 1899 -0.015911195444538048 1999 -0.01512755414717172 2099 -0.014419652551368074 2199 -0.013772095486375625 2299 -0.013179941576847973 2399 -0.01263622946061431 2499 -0.012136535236976859 2599 -0.011673507060527888 2699 -0.011244035558989098 2799 -0.010844459250993976 2899 -0.010471849788373774 2999 -0.01012400105746833 |
#예측한 값 확인
for i in range(4):
print('X:', X[i], "y:", y[i], sigmoid(np.sum(X[i]*w) + b))| X: [0 0] y: [0] 7.0765703582980925e-06 X: [0 1] y: [0] 0.01685800433498835 X: [1 0] y: [0] 0.016892931634238755 X: [1 1] y: [1] 0.9765455899723378 |
5-4) XOR 문제
#입력과 출력 데이터 생성 - 같으면 0 다르면 1
X = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([[0], [1], [1], [0]])
#가중치 초기화
w = tf.random.normal([2], 0, 1) #입력 피처가 2개이므로 가중치도 2개
b = tf.random.normal([1], 0, 1) #편향
#학습
for i in range(3000):
#샘플이 여러 개이므로 에러는 모든 샘플의 에러 합계로 계산
#에러 합계를 저장할 변수
error_sum = 0
#4는 입력 데이터의 개수
for j in range(4):
#출력
output = sigmoid(np.sum(X[j] * w)+ 1*b)
#오차
error = y[j][0] - output
#가중치 업데이트 - 학습률은 0.1
w = w + X[j] * 0.1 * error
#편향 업데이트
b = b + 1 * 0.1 * error
#에러 값을 추가
error_sum += error
#100번 훈련을 할 때 마다 에러의 합계를 출력
if i % 100 == 99:
print(i, error_sum)| 99 0.016761352459349288 199 0.0033813217285643127 299 0.000681716543979527 399 0.00013744418256744773 499 2.769994422202604e-05 599 5.5935759204484015e-06 699 1.125229269538508e-06 799 2.149941442652903e-07 899 1.9544921903147383e-08 999 4.746623760709667e-08 1099 4.746623760709667e-08 1199 4.746623760709667e-08 1299 4.746623760709667e-08 1399 4.746623760709667e-08 1499 4.746623760709667e-08 1599 4.746623760709667e-08 1699 4.746623760709667e-08 1799 4.746623760709667e-08 1899 4.746623760709667e-08 1999 4.746623760709667e-08 2099 4.746623760709667e-08 2199 4.746623760709667e-08 2299 4.746623760709667e-08 2399 4.746623760709667e-08 2499 4.746623760709667e-08 2599 4.746623760709667e-08 2699 4.746623760709667e-08 2799 4.746623760709667e-08 2899 4.746623760709667e-08 2999 4.746623760709667e-08 |
# 일정 epoch 이후에 에러값이 변경되지 않음
#예측한 값 확인
for i in range(4):
print('X:', X[i], "y:", y[i], sigmoid(np.sum(X[i]*w) + b))| X: [0 0] y: [0] 0.5128175691057347 X: [0 1] y: [1] 0.49999997485429043 X: [1 0] y: [1] 0.4871823676059484 X: [1 1] y: [0] 0.47438160794816525 |
- 4개의 출력 결과가 비슷
#가중치 와 편향을 출력
print('가중치:', w)
print("편향:", b)| 가중치: tf.Tensor([-0.10256328 -0.05128161], shape=(2,), dtype=float32) 편향: tf.Tensor([0.05128151], shape=(1,), dtype=float32) |
- 첫 번째 가중치가 두번째 가중치보다 2배 정도 더 크다.
- 첫번째 데이터의 영향력이 커져서 첫번째 데이터에 의해서 값이 결정될 가능성이 높다.
- XOR 문제는 하나의 선으로는 해결할 수 없는 문제
- 이런 경우는 여러 개의 선을 그어서 해결 - Layer를 여러 개 만들어야 한다.
6. MLP
6-1) XOR 문제 해결
import numpy as np
#입력과 출력 데이터 생성 - 같으면 0 다르면 1
X = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([[0], [1], [1], [0]])
#2개의 완전 연결층을 가진 모델을 생성
#units 는 뉴런의 개수이고 activation은 출력을 계산해주는 함수
#input_shape는 맨 처음 입력 층에서 피처의 모양
model = tf.keras.Sequential([
tf.keras.layers.Dense(units=2, activation='sigmoid', input_shape=(2, )),
tf.keras.layers.Dense(units=1, activation='sigmoid')
])
#lr 부분이 에러가 발생하면 learning_rate 로 수정하시면 됩니다.
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=0.1), loss='mse')
#모델을 확인
model.summary() |
# 훈련
#batch_size는 한 번에 연산되는 데이터의 크기(Mini Batch)
history = model.fit(X, y, epochs=10000, batch_size=1)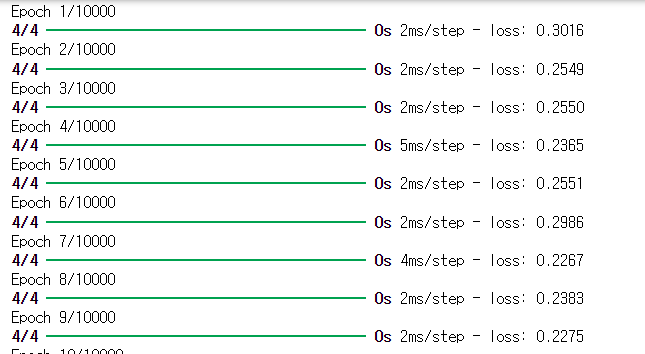 |
# 결과 확인
result = model.predict(X)
print(result) |
# 측정치 변화량 (손실의 변화량)
import matplotlib.pyplot as plt
plt.plot(history.history['loss']) |
7. Tensorflow Data API
- Machine Learning을 하는 경우 대규모 데이터 세트를 사용해야 하는 경우가 있는데 이 경우 Data를 Load 하고 Preprocessing 을 수행하는 작업은 번거로운 작업이며 데이터를 어떻게 사용할 것인가 하는 것도 어려운 작업(Multi Threading, Queue, Batch, Prefetch 등) 중 하나
- Tensorflow Data API
- dataset 객체를 만들고 Data를 읽어올 위치와 변환 방법을 지정하면 이러한 작업을 자동으로 처리
- Data API는 텍스트 파일(csv, tsv 등), 고정 길이를 가진 이진 파일, Tensorflow의 TFRecord 포맷을 사용하는 이진 파일에서 데이터를 읽을 수 있다.
- 관계형 데이터베이스나 Google Big Query 와 같은 NoSQL 데이터베이스에서 데이터를 읽어올 수 있다.
- Tensorflow에서는 One Hot Encoding 이나 BoW Encoding, embedding 등의 작업을 수행해주는 다양한 Preprocessing 층도 제공
7-1) 프로젝트
- TF 변환
- TF Dataset(TFDS)
- dataset을 다운로드할 수 있는 편리한 함수 제공
- 이미지 넷과 같은 대용량 dataset이 포함되어 있음
dataset = tf.data.Dataset.range(10) #0~9 까지의 데이터를 가지고 데이터셋을 구성
print(dataset)| <_RangeDataset element_spec=TensorSpec(shape=(), dtype=tf.int64, name=None)> |
# 대다수의 데이터 셋은 이터레이터 구현
for item in dataset:
print(item)| tf.Tensor(0, shape=(), dtype=int64) tf.Tensor(1, shape=(), dtype=int64) tf.Tensor(2, shape=(), dtype=int64) tf.Tensor(3, shape=(), dtype=int64) tf.Tensor(4, shape=(), dtype=int64) tf.Tensor(5, shape=(), dtype=int64) tf.Tensor(6, shape=(), dtype=int64) tf.Tensor(7, shape=(), dtype=int64) tf.Tensor(8, shape=(), dtype=int64) tf.Tensor(9, shape=(), dtype=int64) |
- 데이터에 마지막이 batch 개수에 맞지 않는 경우 drop_remainder=True를 설정하면 마지막 배치는 사용하지 않음
dataset = dataset.repeat(5).batch(5)
for item in dataset:
print(item)| tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64) tf.Tensor([5 6 7 8 9], shape=(5,), dtype=int64) tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64) tf.Tensor([5 6 7 8 9], shape=(5,), dtype=int64) tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64) tf.Tensor([5 6 7 8 9], shape=(5,), dtype=int64) tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64) tf.Tensor([5 6 7 8 9], shape=(5,), dtype=int64) tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64) tf.Tensor([5 6 7 8 9], shape=(5,), dtype=int64) |
# 데이터 변환
dataset1 = dataset.map(lambda x : x * 2)
for item in dataset1:
print(item)| tf.Tensor([0 2 4 6 8], shape=(5,), dtype=int64) tf.Tensor([10 12 14 16 18], shape=(5,), dtype=int64) tf.Tensor([0 2 4 6 8], shape=(5,), dtype=int64) tf.Tensor([10 12 14 16 18], shape=(5,), dtype=int64) tf.Tensor([0 2 4 6 8], shape=(5,), dtype=int64) tf.Tensor([10 12 14 16 18], shape=(5,), dtype=int64) tf.Tensor([0 2 4 6 8], shape=(5,), dtype=int64) tf.Tensor([10 12 14 16 18], shape=(5,), dtype=int64) tf.Tensor([0 2 4 6 8], shape=(5,), dtype=int64) tf.Tensor([10 12 14 16 18], shape=(5,), dtype=int64) |
# 원하는 데이터만 추출
dataset = tf.data.Dataset.range(10)
dataset = dataset.filter(lambda x : x % 2 == 1)
for item in dataset:
print(item)| tf.Tensor(1, shape=(), dtype=int64) tf.Tensor(3, shape=(), dtype=int64) tf.Tensor(5, shape=(), dtype=int64) tf.Tensor(7, shape=(), dtype=int64) tf.Tensor(9, shape=(), dtype=int64) |
dataset = tf.data.Dataset.range(10)
dataset = dataset.take(3)
for item in dataset:
print(item)| tf.Tensor(0, shape=(), dtype=int64) tf.Tensor(1, shape=(), dtype=int64) tf.Tensor(2, shape=(), dtype=int64) |
# 데이터 shuffling
- 경사하강법은 훈련 세트에 있는 데이터들이 독립적이고 동일한 분포를 가졌을 때 최고의 성능을 발휘
- 셔플링을 할 때 주의할 점은 랜덤 시드를 부여해서 shuffling 되는 순서를 동일하게 만들어야 한다.
dataset = tf.data.Dataset.range(10).repeat(3)
dataset = dataset.shuffle(buffer_size=3, seed=42).batch(7)
for item in dataset:
print(item)| tf.Tensor([0 3 4 2 1 5 8], shape=(7,), dtype=int64) tf.Tensor([6 9 7 2 3 1 4], shape=(7,), dtype=int64) tf.Tensor([6 0 7 9 0 1 2], shape=(7,), dtype=int64) tf.Tensor([8 4 5 5 3 8 9], shape=(7,), dtype=int64) tf.Tensor([7 6], shape=(2,), dtype=int64) |
- https://tensorflow.org/datasets 에 가면 널리 사용되는 dataset을 다운로드 할 수 있음
- tfds.load 함수를 호출하면 Data를 다운로드하고 dataset 의 디셔너리로 Data를 리턴
- minist 데이터 가져오기
#!pip install tensorflow_datasets
import tensorflow_datasets as tfds
datasets = tfds.load(name="mnist")
#dict 형태로 데이터를 가져옵니다.
print(type(datasets))
#모든 키 확인
print(datasets.keys())
print(type(datasets['train'])) |
#하나의 데이터도 dict 로 되어 있음
for item in datasets['train']:
#print(type(item))
#print(item.keys())
#print(item['label'])
plt.imshow(item['image'])
break |
'Python' 카테고리의 다른 글
| [Python] 딥러닝 _ Keras (0) | 2024.03.20 |
|---|---|
| [Python] 연관 분석 (0) | 2024.03.18 |
| [Python] 연관분석 실습 _ 네이버 지식인 크롤링 (4) | 2024.03.15 |
| [Python] 감성 분석 실습 (3) | 2024.03.14 |
| [Python] 차원 축소 (0) | 2024.03.12 |
